Lean 문법 입문서

AI & ML-ops•2025.11.19

overreacted 블로그 포스트 번역

원문: https://overreacted.io/a-lean-syntax-primer/

이것은 Lean 프로그래밍 언어에 대한 제 개인적인 문법 입문서입니다. 완전하지는 않으며 부정확한 부분이 있을 수 있습니다(저도 아직 Lean을 배우고 있습니다). 하지만 이것이 제가 Lean에 처음 소개받고 싶었던 방식이며, 명확히 해주기를 원했던 내용입니다.

Lean을 왜 배워야 할까요?

이 글은 이미 Lean을 배우고 싶은 마음이 있다고 가정합니다. 동기 부여를 위해 두 가지 관점을 제시합니다: 제 관점과 그 창시자의 관점.

정의 선언하기

먼저 몇 가지 정의를 작성해봅시다. 이들은 파일의 최상위 레벨에 나타날 수 있습니다:

def name := "Alice"
def age := 42

(온라인 플레이그라운드에서 시도해보세요.)

:=(할당)을 사용해야 하며 =는 사용할 수 없습니다. 이는 Lean이 비교를 위해 =를 사용하기 때문입니다. 이는 Go나 Pascal(충분히 나이가 많다면)을 떠올리게 할 수 있습니다.

명시적으로 타입을 작성하지 않았지만, 각 정의는 타입이 지정됩니다. 타입을 알아보려면 온라인 플레이그라운드에서 name과 age 위에 마우스를 올리거나 VS Code 내에서 확인할 수 있습니다. name : String과 42 : Nat이 표시되어야 합니다. (앞으로 "마우스를 올린다"고 말할 때는 이 두 환경 중 하나를 가정하겠습니다.)

여기서 String은 명백히 문자열이고, Nat은 "자연수"를 의미합니다. Lean에서 자연수는 0, 1, 2 등을 포함하며 임의로 큰 수까지 갈 수 있습니다.

:= 앞에 : SomeType을 작성하여 타입을 명시적으로 지정할 수 있습니다:

def name : String := "Alice"
def age : Nat := 42

지정하지 않으면 Lean이 우측에 작성한 내용으로부터 타입을 추론하려고 시도합니다.

타입 지정하기

Lean이 "Alice"를 String으로, 42를 Nat으로 추론한다는 것을 방금 봤습니다. Nat은 0, 1, 2 등이 될 수 있습니다. -140과 같은 음수를 시도하면 어떻게 될까요?

def temperature := -140

temperature 위에 마우스를 올리면 Int임을 알 수 있습니다. Int는 정수를 의미하며, 음수 또는 양수인 모든 정수를 허용하는 내장 타입입니다.

정의에서 Int와 같은 특정 타입을 명시적으로 요청할 수 있습니다:

def roomTemperature : Int := 25

def roomTemperature := 25만 작성했다면 Lean은 Nat을 제공했을 것이지만, : Int를 추가하면 타입 추론이 Int를 생성하도록 유도합니다.

특정 타입을 요청하는 또 다른 방법은 표현식 자체를 감싸는 것입니다:

def roomTemperature := (25 : Int)

두 경우 모두 정말로 Int를 원한다고 말하는 것입니다. Lean이 표현식으로부터 Int를 생성하는 방법을 알아낼 수 없다면 타입 오류를 줄 것입니다.

Alice의 출생 연도를 그녀의 나이를 기반으로 계산해봅시다:

def name := "Alice"
def age := 42
def birthYear := 2025 - age

birthYear를 어딘가에 화면에 표시해야 합니다. 온라인 플레이그라운드를 따라가고 있다면 코드가 실제로 실행되지 않는다는 것을 깨달을 수 있습니다.

이는 Lean을 사용하는 두 가지 방법이 있기 때문입니다.

Lean을 사용하는 한 가지 방법은 코드를 실행하는 것입니다. 또 다른 방법은 코드에 대한 사실을 증명하는 것입니다. 둘 다 할 수도 있습니다 — 코드를 작성하고 그에 대한 증명을 작성합니다. 먼저 코드를 실행하는 방법을 배우고, 그 다음 증명을 작성하는 방법을 살펴보겠습니다.

코드 실행하기

어떤 표현식의 결과를 보고 싶다면 #eval 명령을 추가하세요:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
#eval birthYear

이 #eval에 마우스를 올리면 1983이 표시됩니다. 또 다른 표시 위치는 온라인 플레이그라운드의 오른쪽 InfoView입니다: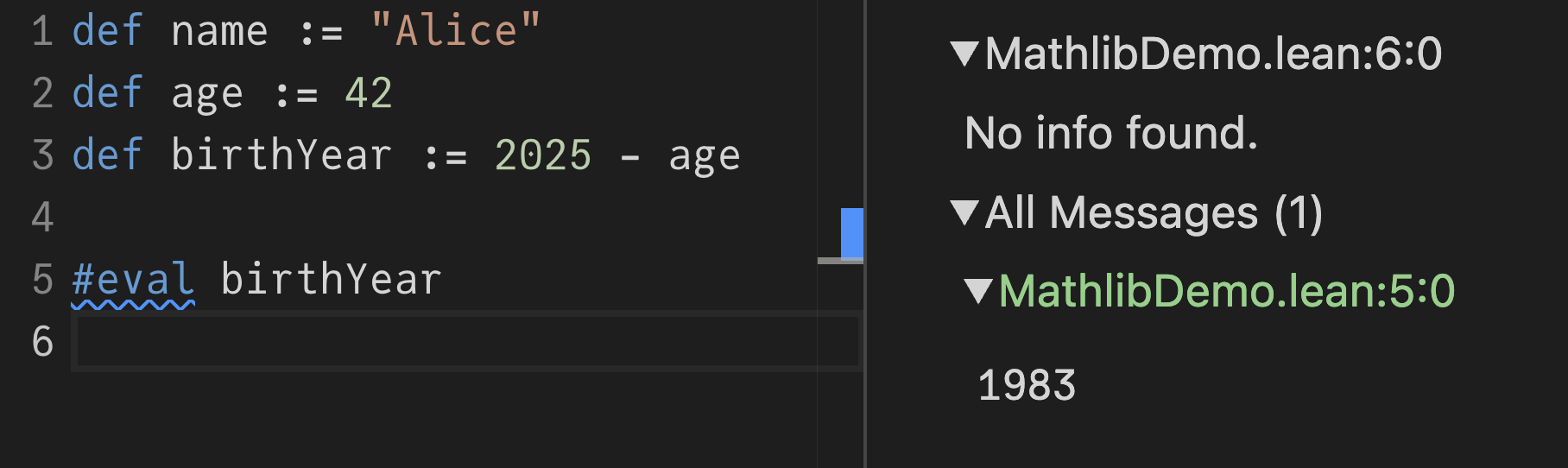

오른쪽 아래 모서리에 1983이 표시됩니다. 로컬에서 Lean 확장으로 VS Code를 설정했다면 다음과 같이 동일한 InfoView를 표시할 수 있습니다:

Lean InfoView는 매우 유용하며 항상 열어두기를 권장합니다.

#eval 명령은 인라인 계산을 수행하고 코드가 의도대로 작동하는지 확인하는 데 편리합니다. 하지만 실제로 뭔가를 출력하는 프로그램을 실행하고 싶을 수도 있습니다. main을 정의하여 Lean 파일을 실제 프로그램으로 만들 수 있습니다:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
def main := IO.println birthYear

의도적으로 "main 함수"라고 말하지 않았습니다. main은 함수가 아니기 때문입니다. (마우스를 올려서 main의 타입을 배울 수 있지만 오늘은 그에 집중하지 않겠습니다.)

프로그램을 실행해봅시다:

lean --run Scratch.lean

이제 1983이 터미널에 나타납니다. 또는 다음과 같이 할 수도 있습니다:

lean Scratch.lean -c Scratch.c

Lean 컴파일러가 생성한 C 코드는 1983을 출력하는 명령을 포함할 것입니다:

LEAN_EXPORT lean_object* _lean_main(lean_object* x_1) {
  lean_object* x_2; lean_object* x_3;
  x_2 = lean_unsigned_to_nat(1983u);
  x_3 = l_IO_println___at___main_spec__0(x_2, x_1);
  return x_3;
}

이제 Lean을 사용하여 프로그램을 작성할 수 있다는 것을 알 수 있습니다.

증명 작성하기

이제 age + birthYear가 함께 2025에 더해진다는 것을 증명해봅시다.

프로그램과 함께 작은 theorem을 정의하세요:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
theorem my_theorem : age + birthYear = 2025 := by
  sorry

theorem은 def와 유사하지만 증명을 선언하기 위해 특별히 목표합니다.

정리의 선언된 타입은 그것이 증명해야 할 명제입니다. 이제 당신의 일은 그 타입의 증명을 구성하는 것이며, Lean "tactic 모드"(by로 활성화됨)는 그러한 증명을 구성하는 대화형이고 간결한 방법을 제공합니다.

처음에 InfoView는 당신의 목표가 age + birthYear = 2025라고 말합니다: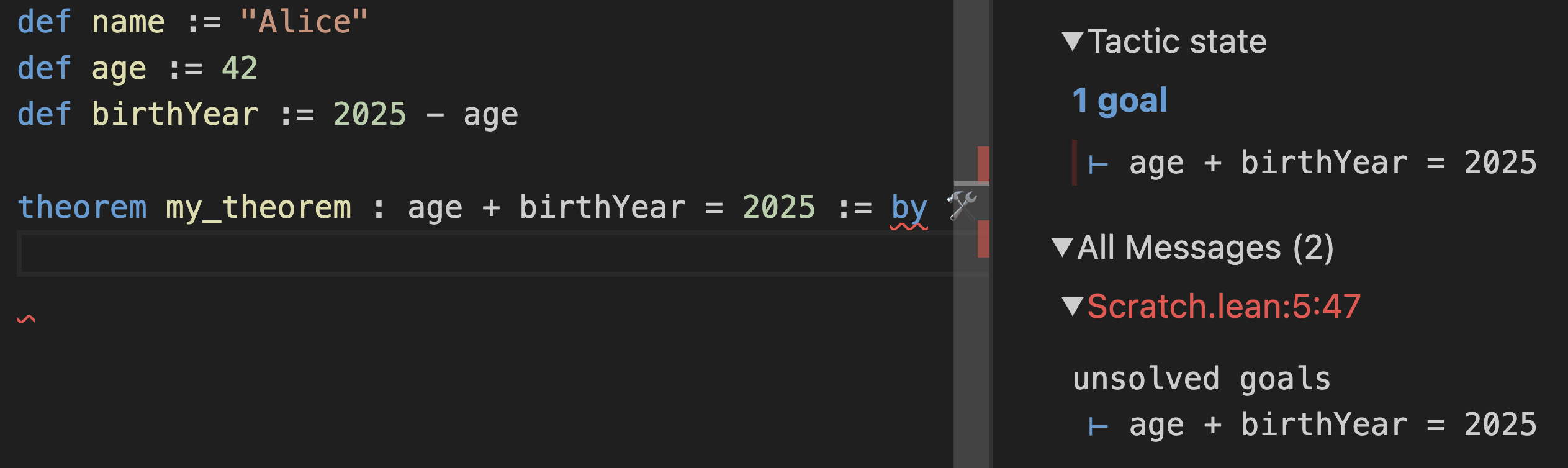

하지만 그것은 직접 확실할 수 있는 것이 아닙니다. age가 뭐죠? unfold age를 시도하여 목표에서 age를 그 정의가 말하는 것으로 바꾸세요: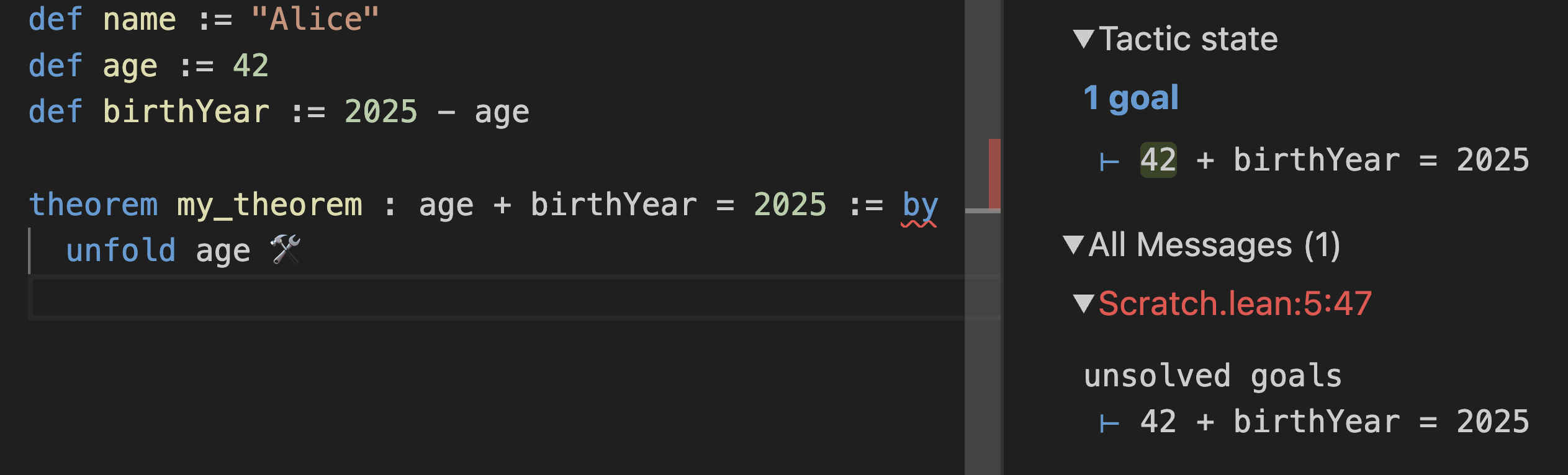

InfoView의 목표가 42 + birthYear = 2025로 어떻게 변했는지 주목하세요. 좋아요, 하지만 birthYear가 뭐죠? unfold birthYear도 해봅시다:

거의 다 왔습니다; 목표는 이제 42 + (2025 - age) = 2025입니다. birthYear를 펼치면 age가 다시 나타났습니다. age가 뭐죠? unfold age를 해봅시다: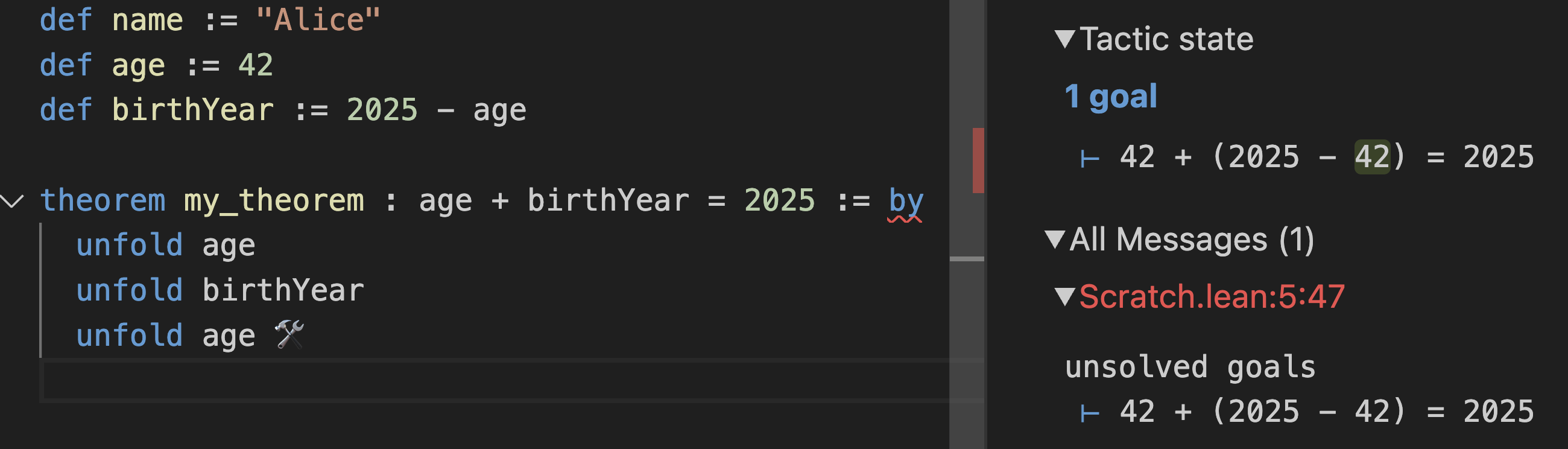

이 시점에서 목표는 42 + (2025 - 42) = 2025이며, 이는 간단한 산술 표현식입니다. 내장된 decide tactic은 이를 쉽게 풀 수 있습니다: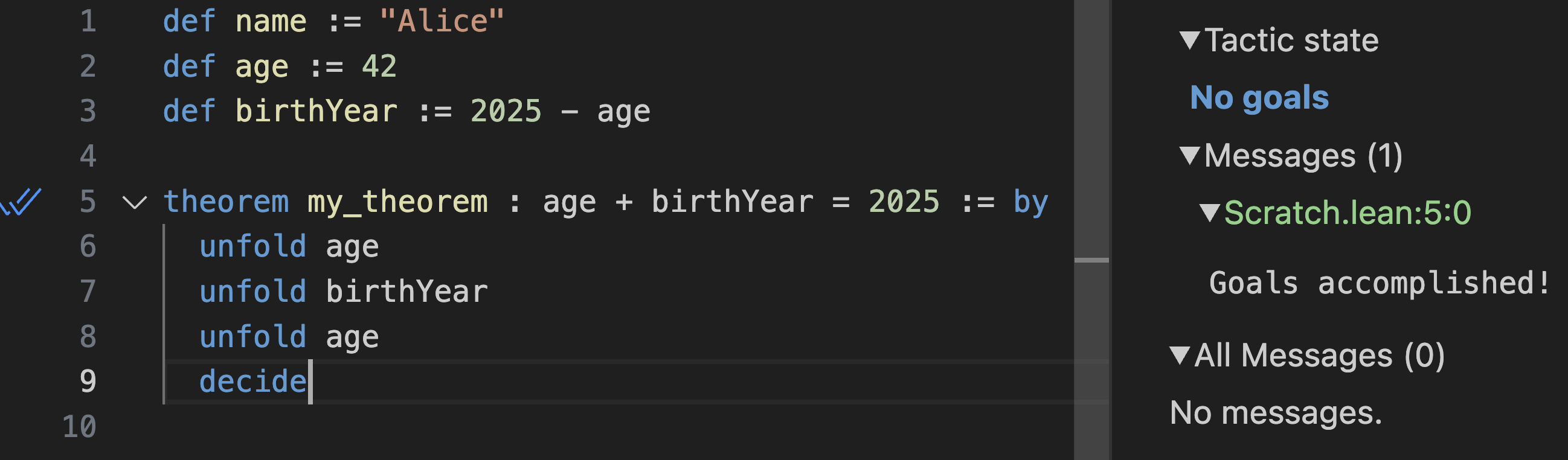

완료했습니다! 실제로 코드를 실행하지 않고 age + birthYear = 2025를 증명했습니다. 이는 타입 검사 중에 검증됩니다.

age를 다른 숫자로 편집해도 증명이 무효화되지 않는다는 것을 확인할 수 있습니다. 하지만 birthYear를 2023 - age로 편집하면 증명이 더 이상 타입 검사를 통과하지 않습니다: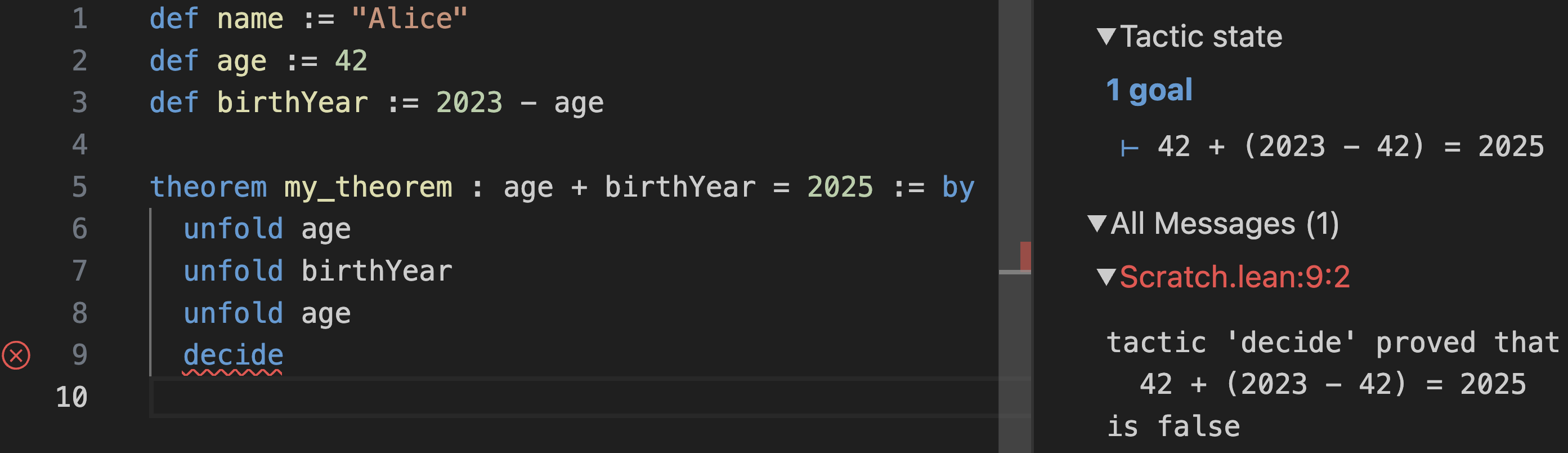

tactic 'decide' proved that 42 + (2023 - 42) is false

물론 이 모든 것이 좀 장황했습니다. 각 정의에 대해 수동으로 unfold를 하는 대신, simp 단순화기에 재귀적으로 수행하도록 지시할 수 있습니다: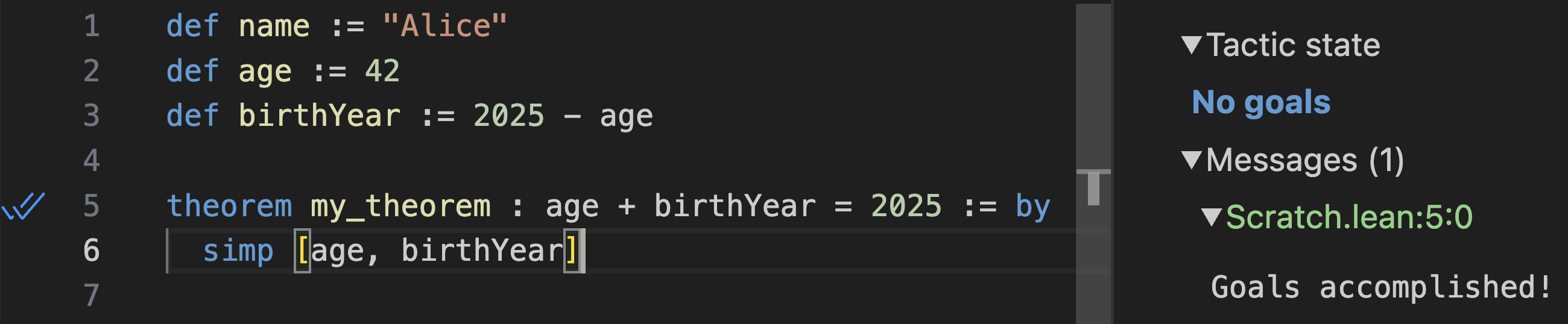

simp [age, birthView] solves the same theorem

이것도 목표를 증명합니다.

이 예제는 인위적이지만 단계별로 코드를 진행하고 "바깥쪽에서 안쪽으로" 변환하는 느낌을 보여주고 싶었습니다. 거의 당신이 컴퓨터인 것처럼 느껴지며, 논리적으로 코드를 목표로 변환합니다. 특히 준비된 유용한 정리가 있으면 항상 그렇게 지루하지는 않을 것입니다.

증명에 대해 다시 돌아올 것이지만, 지금은 더 많은 Lean 기초를 배워봅시다.

네임스페이스 열기

이 main 정의를 다시 살펴보세요:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
def main := IO.println birthYear

여기서 IO.println birthYear는 함수 호출입니다. IO는 네임스페이스이고, println은 그 네임스페이스에 정의된 함수입니다. birthYear를 전달합니다.

IO 네임스페이스를 열어서 IO. 앞에 쓸 필요를 피할 수 있습니다:

open IO
def name := "Alice"
def age := 42
def birthYear := 2025 - age
def main := println birthYear

이것은 파일의 맨 위에 있을 필요가 없습니다:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
open IO
def main := println birthYear

이제 open IO 위에는 IO.println을 작성해야 하지만 아래에는 println을 직접 작성할 수 있다는 것이 혼란스러울 수 있습니다. 대안으로, in을 추가하여 IO 열기를 특정 정의로 범위를 지정할 수 있습니다:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
open IO in
def main := println birthYear

이렇게 하면 더 짧은 구문을 main 내에서 사용할 수 있지만 외부에서는 사용할 수 없습니다.

우리는 IO를 많이 사용하지 않으므로 아래에서 println을 IO.println으로 계속 참조하겠습니다.

인수 전달하기

이제 birthYear를 println 함수에 전달하는 방법을 주목하세요:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
def main := IO.println birthYear

JavaScript와 같은 언어와 달리 Lean은 함수 호출에 괄호나 쉼표를 사용하지 않습니다. f(a, b, c) 대신 Lean에서는 f a b c를 작성합니다.

이것을 강조하고 싶습니다. 함수 호출에 쉼표와 괄호가 사용되지 않습니다!

하지만 개별 인수 주위에 괄호를 사용할 수도 있습니다. birthYear를 함수 호출에서 2025 - age로 직접 바꾼다고 가정하세요:

def name := "Alice"
def age := 42
def main := IO.println 2025 - age

이것은 오류를 초래합니다:

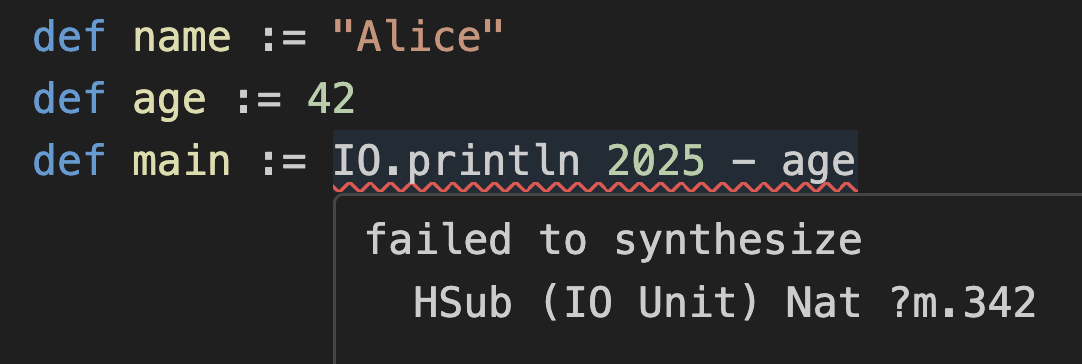
Failed to synthesize HSub (IO Unit) Nat ?m.342

Lean은 (IO.println 2025) - age를 하려고 생각하므로, age(이는 Nat)를 IO.println 2025가 반환하는 것(이는 IO Unit이라고 불리는 것)에서 빼는 방법을 찾습니다. Lean은 IO Unit과 Nat 사이의 빼기 연산(HSub)을 찾을 수 없으므로 좌절해서 포기합니다.

이를 해결하려면 2025 - age 주위에 괄호를 추가하세요:

def name := "Alice"
def age := 42
def main := IO.println (2025 - age)

이제 IO.println이 2025 인수를 "먹는" 대신, 첫 번째 인수가 전체 (2025 - age) 표현식임을 알 수 있습니다. (와 ) 괄호를 자유롭게 사용하고 제거해보면서 언제 필요한지 느껴보는 것이 도움이 될 수 있습니다.

(와 ) 괄호는 여기서 IO.println 함수 호출과 아무 관련이 없습니다. 유일한 목적은 2025 - age를 "그룹화"하는 것이며, 수학에서 물건을 그룹화하는 것처럼입니다.

다시 말해, JavaScript에서 something(f(x, y), a, g(z))를 작성하는 대신 Lean에서는 something (f x y) a (g z)를 작성합니다.

이것을 여러 번 자세히 읽고 깊은 잠재의식에 새겨지도록 하세요.

표현식 중첩하기

Lean 정의를 중첩할 수 없습니다. 하지만 일부 정의가 복잡해지면 정의 내에서 let 바인딩을 선언하여 단순화할 수 있습니다.

예를 들어, 마지막 예제에서 (2025 - age)를 let으로 끌어낼 수 있습니다:

def name := "Alice"
def age := 42
def main :=
  let birthYear := 2025 - age
  IO.println birthYear

다시 한 번, 할당에 :=를 사용합니다. =가 아니라 :=입니다!

main이 다중 라인이라고 해서 함수가 되는 것은 아닙니다. let 바인딩을 추가하는 것은 정의를 읽기 쉽게 만드는 방법일 뿐입니다. name과 age 정의를 포함한 모든 정의 내에서 let을 사용할 수 있습니다:

def name :=
  let namesInPassport := ["Alice", "Babbage", "McDuck"]
  namesInPassport[0]
def age :=
  let twenty := 20
  let one := 1
  twenty + twenty + one + one
def main :=
  let birthYear := 2025 - age
  IO.println birthYear

여기서 return 문이 필요하지 않습니다. 정의의 마지막 라인이 그 값이 됩니다. 이것이 위의 정의가 다음과 동등한 이유입니다:

def name := ["Alice", "Babbage", "McDuck"][0]
def age := 20 + 20 + 1 + 1
def main := IO.println (2025 - age)

결국 모든 정의의 우측은 단일 표현식으로 펼쳐지지만, let은 그 표현식을 더 읽기 쉽고 재사용 가능한 조각으로 나눌 수 있게 해줍니다.

함수 선언하기

현재 birthYear는 계산에 2025를 하드코딩합니다:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
def main := IO.println birthYear

def birthYear 뒤에 공백을 두고 currentYear 인수를 선언하여 birthYear를 함수 정의로 바꿀 수 있습니다:

def name := "Alice"
def age := 42
def birthYear currentYear := currentYear - age

이렇게 하면 birthYear가 함수가 됩니다. birthYear 2025를 작성하여 호출할 수 있습니다:

def name := "Alice"
def age := 42
def birthYear currentYear := currentYear - age
def main := IO.println (birthYear 2025)

다시 한 번, birthYear 2025 주위의 괄호는 IO.println이 birthYear 함수 자체를 "먹으려고" 하지 않도록 합니다. 우리는 그것이 birthYear 2025를 "먹기"를 원합니다.

이제 birthYear 위에 마우스를 올리면 타입이 더 이상 Nat이 아님을 알 수 있습니다: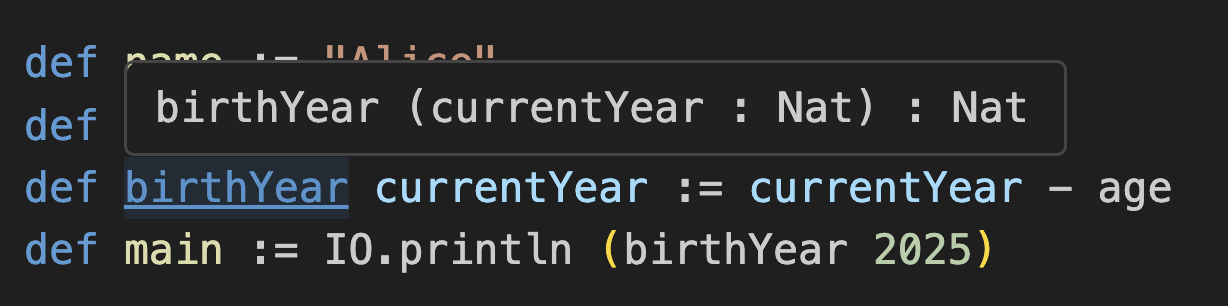

이것이 Lean이 함수 타입을 예쁘게 출력하는 방식입니다. 함수 이름 birthYear, 그 인수(우리는 하나만 가짐), : 그리고 반환 타입을 봅니다.

의도한 타입을 명확히 하기 위해 명시적으로 작성할 수도 있습니다:

def birthYear (currentYear : Nat) : Nat := currentYear - age

다시 한 번, Lean의 ( ) 괄호는 함수 호출과 아무 관련이 없습니다. (currentYear : Nat)을 단일 항목으로 취급하기 위해서만 괄호를 사용합니다.

함수를 선언하는 많은 방법들

같은 함수를 정의하는 두 가지 방법을 봤습니다. 암시적 타입과 명시적 타입:

/-- Types are implicit here, Lean infers them -/
def birthYear currentYear := currentYear - age
/-- Types are explicit here -/
def birthYear (currentYear : Nat) : Nat := currentYear - age

같은 birthYear 함수를 정의하는 더 많은 유효한 방법들이 있으며, 다양한 수준의 상세함이 있습니다. 다음은 같은 birthYear 함수를 정의하는 (완전하지 않은) 방법들의 목록입니다:

/-- Concise definition -/
def birthYear currentYear := currentYear - age
def birthYear (currentYear: Nat) := currentYear - age
def birthYear (currentYear: Nat) : Nat := currentYear - age
/-- Definition set to an anonymous function -/
def birthYear := fun currentYear => currentYear - age
def birthYear := fun (currentYear: Nat) => currentYear - age
/-- Definition (with explicit type) set to an anonymous function -/
def birthYear : Nat → Nat := fun currentYear => currentYear - age

이것은 JavaScript의 function f() {}와 const f = () => ...를 떠올리게 할 수 있습니다. 저는 간결한 문법이 가장 읽기 좋다고 생각하며, 특히 익명 함수가 필요한 경우(예: 다른 함수에 전달하기 위해)가 아니면 사용하기를 권장합니다.

여기서 Nat → Nat은 어떤 문법을 사용하든 birthYear의 실제 타입입니다. Nat을 받아서 Nat을 반환하므로 Nat → Nat입니다. 멋진 → 화살표는 플레이그라운드에서 \to 뒤에 공백을 입력하거나 Lean VSCode에서 입력합니다.

인수 타입을 지정하지만 반환을 추론하는 것은 종종 좋은 중간 지점입니다:

def birthYear (currentYear: Nat) := currentYear - age

JavaScript의 function 선언과 화살표 함수처럼, 각 경우에 원하는 상세함과 타입 지정의 수준은 대부분 당신에게 달려 있습니다.

(참고: fun x ↦ x * 2 같은 문법도 볼 수 있으며, fun x => x * 2 대신입니다. 여기서 ↦는 \maps로 입력되며, 수학자들은 미학적으로 =>를 선호합니다. Lean은 이들을 구분하지 않으므로 Lean 자체 같은 코드베이스에서는 =>를 보고 Mathlib 같은 "수학적인" 코드베이스에서는 ↦를 봅니다. 둘 다 fun과 함께 작동합니다.)

인수 추가하기

이제 함수를 작성하는 수십 가지 방법을 알았으니, 이것으로 돌아가봅시다:

def name := "Alice"
def age := 42
def birthYear currentYear := currentYear - age
def main := IO.println (birthYear 2025)

age를 birthYear 함수의 인수로 만들고 싶다고 가정하세요. 인수를 추가하려면 def birthYear 정의 인수 목록에 다음을 작성하세요:

def name := "Alice"
def birthYear currentYear age := currentYear - age
def main := IO.println (birthYear 2025 42)

실제로 이것은 작동하지 않으며, 오류가 좋지 않습니다.

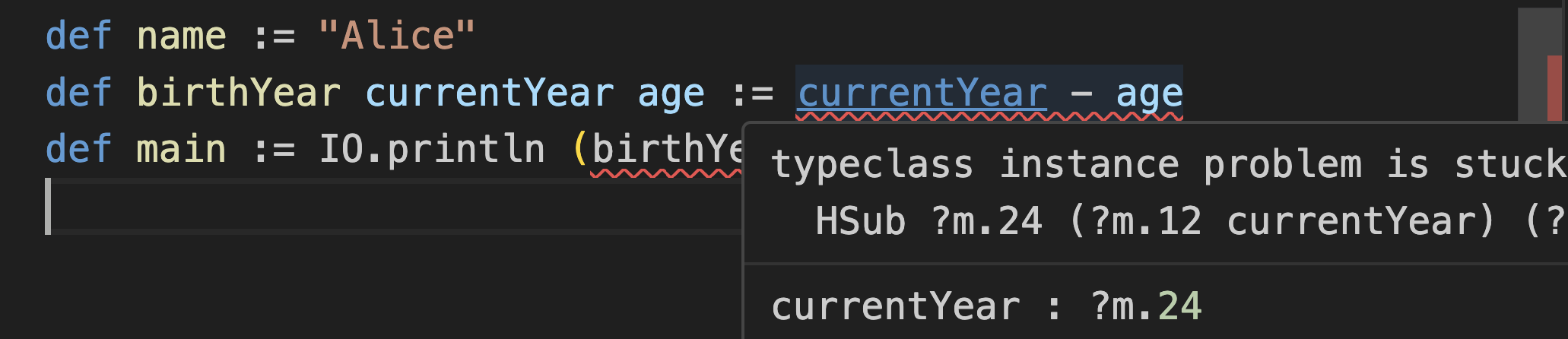
문제는 제가 앞서 설명한 문제입니다 — 이 시점에서 Lean은 currentYear과 age의 타입이 무엇인지 전혀 모릅니다. 이전에는 age가 이전 선언이라는 사실에 의존했고(그리고 Nat으로 추론했지만) 이제 Lean은 정말 막혔습니다.

이상한 오류 메시지("typeclass instance is stuck")는 두 타입 사이의 빼기 구현을 찾으려고 시도하고 있다는 사실을 암시합니다(그 구현을 찾는 것은 "typeclass 검색"을 통해 수행됨). 하지만 그것들이 무엇인 타입인지도 모릅니다(그래서 이상한 ?m.24와 ?m.12 플레이스홀더를 봅니다).

이것을 해결하는 방법은 총알을 깨물고 실제로 타입을 지정하는 것입니다:

def name := "Alice"
def birthYear (currentYear : Nat) (age : Nat) :=
  currentYear - age
def main := IO.println (birthYear 2025 42)

이제 모호함이 없습니다. 괄호는 여기서 특별한 의미가 없습니다 — 각 매개변수를 서로 분리하는 방법일 뿐입니다. 함수를 호출할 때처럼, 우리는 쉼표를 사용하지 않으므로 그룹화를 위해 괄호가 필요합니다.

같은 타입의 여러 매개변수가 연속으로 있을 때, 위의 currentYear과 age처럼, 하나의 타입 선언 아래에 함께 놓을 수 있습니다:

def name := "Alice"
def birthYear (currentYear age : Nat) :=
  currentYear - age
def main := IO.println (birthYear 2025 42)

이것은 의미론을 변경하지 않지만 작성하기가 더 짧습니다. 이것은 특히 모두 Nat 같은 3개 또는 4개의 매개변수가 있을 수 있는 수학에서 유용합니다.

이제 모든 매개변수 타입을 명시적으로 지정하고 있으므로, 그들에 대해 더 열심히 생각하고 약간 다른 타입을 주는 것이 합리적입니다. age는 Nat으로 남아야 하지만, currentYear은 BC 시대에 태어난 사람들이나 2000년 이상 된 사람들을 위해 계산이 여전히 작동하도록 Int로 더 합리적입니다.

def name := "Alice"
def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age
def main := IO.println (birthYear 2025 42)

birthYear의 비-예쁜-형식 타입은 Int → Nat → Int입니다. Int를 받고 Nat도 받으며 Int를 반환하기 때문입니다. 다른 함수형 언어처럼, 부분적으로 적용할 수 있습니다 — 예를 들어, birthYear 2025는 나중에 남은 age 인수로 호출할 수 있는 Nat → Int 함수를 제공합니다.

이제 Int와 Nat을 받는 같은 함수를 정의하는 다른 점점 더 미친 동등한 방법들이 있을 수 있다고 추측했을 것입니다:

def birthYear (currentYear : Int) (age : Nat) := currentYear - age
def birthYear (currentYear : Int) := fun (age : Nat) => currentYear - age
def birthYear := fun (currentYear : Int) (age : Nat) => currentYear - age
def birthYear := fun (currentYear : Int) => fun (age : Nat) => currentYear - age
def birthYear: Int → Nat → Int := fun currentYear age => currentYear - age
def birthYear: Int → Nat → Int := fun currentYear => fun age => currentYear - age

그들이 모두 Lean에서 정확히 동등하다는 것을 염두에 두고 자세히 읽으세요. 단일 정의 내에서 문법을 혼합하는 것은 혼란스러우므로 이것을 고수하겠습니다:

def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age

증명을 다시 살펴볼 시간입니다.

모든 것에 대해 증명하기

몇 섹션 전에, 이 코드에 대해 birthYear + age = 2025를 증명했습니다:

def name := "Alice"
def age := 42
def birthYear := 2025 - age
theorem my_theorem : age + birthYear = 2025 := by
  simp [age, birthYear]

하지만 이제 birthYear는 두 개의 인수를 받는 함수입니다:

def name := "Alice"
def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age

age와 currentYear의 구체적인 값에 대해 이 정리를 복사-붙여넣기할 수 있습니다:

def name := "Alice"
def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age
theorem my_theorem : 42 + birthYear 2025 42 = 2025 := by
  simp [birthYear]
theorem my_theorem' : 25 + birthYear 2025 25 = 2025 := by
  simp [birthYear]
theorem my_theorem'' : 77 + birthYear 1980 77 = 1980 := by
  simp [birthYear]

이 증명들은 타입 검사를 통과하지만, 테스트를 작성하는 것보다 나을 것이 없다는 느낌이 있습니다. 우리가 포착하고 싶은 것은 보편적인 패턴이지, 많은 경우들이 아닙니다.

사실, cy(저는 "current year"을 줄여서 그렇게 부르겠습니다)와 a(짧게 "age")가 무엇이든, a + birthYear cy a는 cy와 같아야 합니다. 그것을 포착해봅시다:

def name := "Alice"
def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age
theorem my_theorem : a + birthYear cy a = cy := by
  sorry

a와 cy를 선언하지 않았지만, 이것은 실제로 유효한 문법입니다! VS Code Lean 확장은 암시적으로 my_theorem 뒤에 {a cy} 인수를 삽입합니다: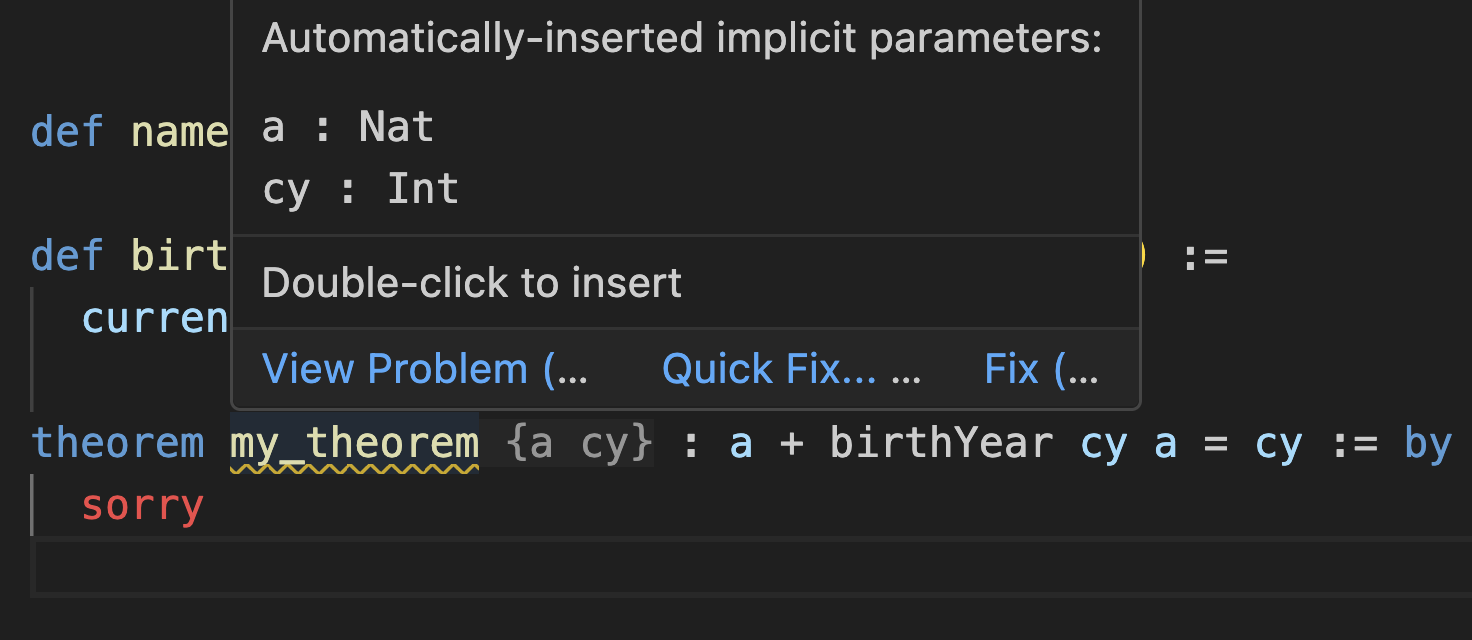

Automatically inserted implicit arguments: a : Nat, cy : Int

이 { } 중괄호로 둘러싼 "암시적" 인수는 때때로 매우 유용할 수 있지만, 이 경우 도움이 되는 것보다 더 혼란스럽습니다. my_theorem의 일반 인수로 cy와 a를 명시적으로 선언해봅시다:

def name := "Alice"
def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age
theorem my_theorem (cy : Int) (a : Nat) : a + birthYear cy a = cy := by
  sorry

함수 인수를 선언하는 것과 유사하게 my_theorem을 cy와 a로 선언하는 방법을 주목하세요 — 단, 실제로 이 정리를 "실행"할 수는 없습니다. 당신은 단지 cy와 a에 대해, a + birthYear cy a = cy의 증명을 생성할 수 있다고 말하고 있습니다.

실제로 할 수 있는지 봅시다!

↑a + birthYear cy a = cy 목표로 시작합니다: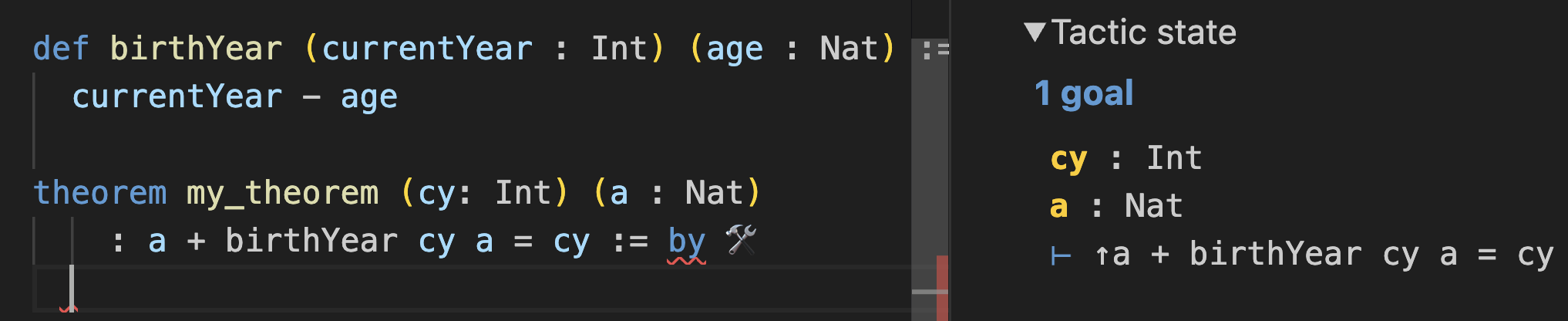

앞의 ⊢ 기호는 이것이 목표, 즉 증명하고 싶은 것임을 알려줍니다. 그 위의 것들, cy : Int와 a : Nat 같은 것들은 당신이 이미 가지고 있는 것들입니다.

당신은 궁금해할 수 있습니다: cy : Int와 a : Nat이 무엇인가. 그들의 값이 무엇인가? 하지만 그 질문은 의미가 없습니다. 당신은 증명을 작성하고 있으므로, 어떤 의미에서 당신은 동시에 모든 가능한 값으로 작업하고 있습니다. 당신은 그들의 타입만 가지고 있습니다.

목표를 다시 살펴보세요: ↑a + birthYear cy a = cy.

그 위 화살표가 뭐죠?

InfoView에서 마우스를 올려보세요:

서명이 좀 혼란스럽습니다(@가 뭐죠? instNatCastInt가 뭐죠?). 하지만 당신의 a(Nat임)를 받아서 Int를 반환한다는 것을 볼 수 있습니다. 따라서 이것이 Lean이 당신의 a가 Int로 변환되고 있다는 사실을 표시하는 방식이므로, 그것이 birthYear cy a 호출의 결과(이미 Int)와 더해질 수 있습니다.

좋아요, 목표는 ↑a + birthYear cy a = cy를 증명하는 것입니다. 어떻게 할까요?

음, 먼저 unfold birthYear를 해서 구현으로 바꿔봅시다: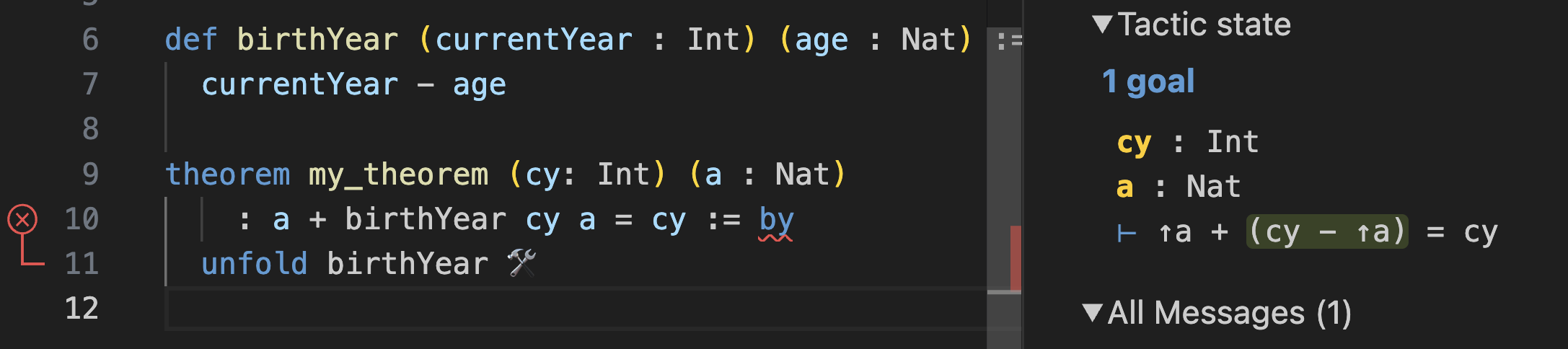

이제 목표는 ↑a + (cy - ↑a) = cy가 됩니다.

이전의 decide tactic을 사용할 수 없습니다. 왜냐하면 그것은 알려진 구체적인 숫자만 다루기 때문입니다 — 계산기처럼입니다. 하지만 Lean은 또한 a와 cy 같은 미지수를 포함하는 방정식을 확인할 수 있는 omega tactic을 포함합니다.

omega를 사용하면 이 증명을 완료할 수 있습니다!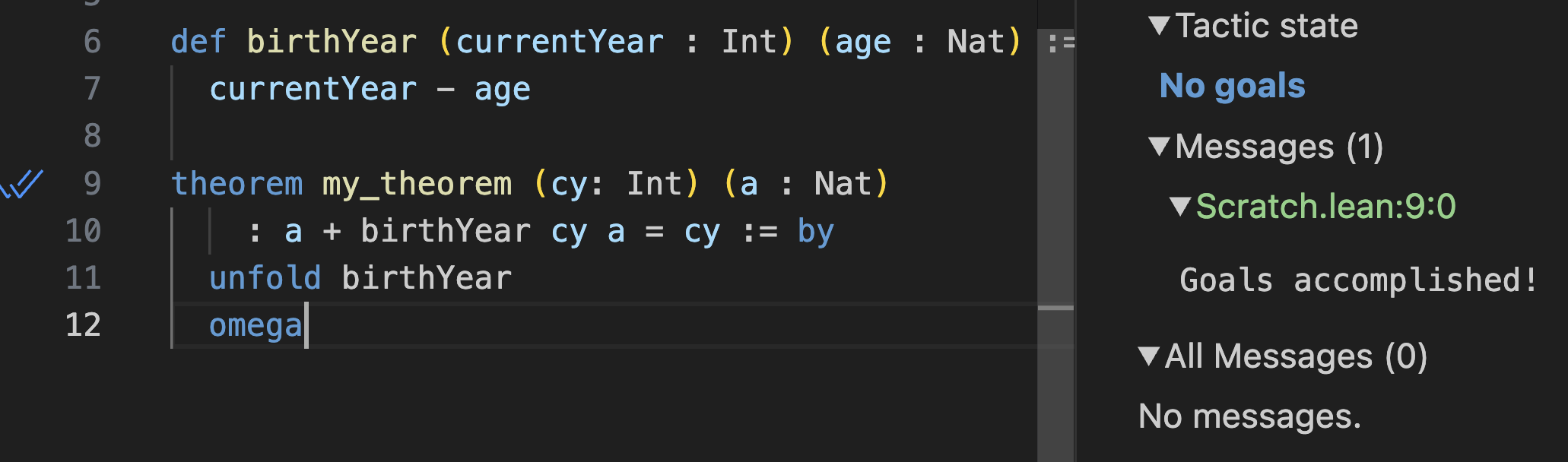

전체 코드를 다시 살펴봅시다:

def name := "Alice"
def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age
theorem my_theorem (cy: Int) (a : Nat) : a + birthYear cy a = cy := by
  unfold birthYear
  omega

birthYear 함수와 그 동작에 대한 my_theorem 정리가 있습니다. 관례상, birthYear_spec 또는 age_add_birthYear_eq_current_year 같은 더 구체적인 것으로 부르고 싶을 수 있습니다.

어떤 의미에서 그것은 테스트와 같지만, 그 함수의 모든 가능한 입력에 대한 테스트이며 타입 검사 중에 실행됩니다. 저는 이것이 매우 멋있다고 생각합니다. birthYear의 공식을 잘못 변경하면 증명이 더 이상 타입 검사를 통과하지 않는다는 것을 확인할 수 있습니다: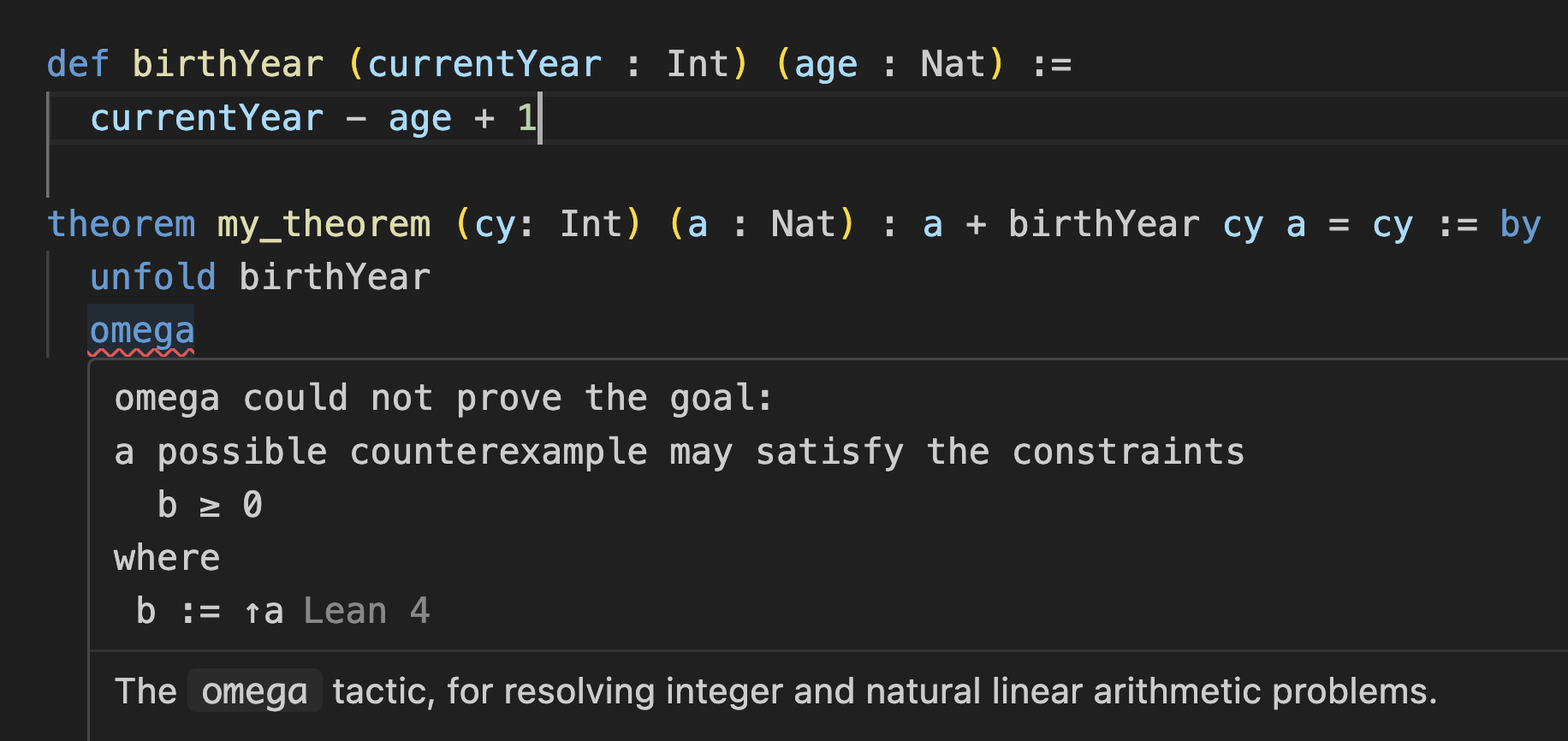

전칭 한정자

이전에 my_theorem의 인수로 cy와 a를 선언했습니다:

theorem my_theorem (cy: Int) (a : Nat) : a + birthYear cy a = cy := by
  unfold birthYear
  omega

이 경우, birthYear 호출 자체로부터 타입을 정확히 추론할 수 있으므로 타입을 생략하는 것이 좋습니다. 이미 명시적으로 주석을 달았습니다:

theorem my_theorem cy a : a + birthYear cy a = cy := by
  unfold birthYear
  omega

이 정리는 "모든 cy와 a에 대해, a + birthYear cy a는 cy와 같다"고 말합니다. 수학자들은 전칭 한정자 ∀(모든 것을 의미함)를 사용하여 이와 같은 명제를 작성하는 자신만의 방법을 가지고 있습니다: ∀ cy a, a + birthYear(cy, a) = cy.

수학자의 스타일로 ∀ 한정자를 사용하여 위를 다시 표현할 수 있습니다:

theorem my_theorem : ∀ cy a, a + birthYear cy a = cy := by
  sorry

∀를 입력하려면 \all을 입력하고 스페이스를 누르세요.

이제 cy a :대신 : ∀ cy a를 가집니다. 전칭 한정자는 인수를 "나중에" 도입할 수 있게 해줍니다 — 프로그래밍의 커링처럼. 하지만 차이는 대부분 스타일입니다. 정리 서명은 동일합니다.

∀를 사용할 때, 당신은 보편적인 명제("모든 cy와 a에 대해")로 시작하므로 cy와 a는 아직 tactic 상태에 없습니다. intro cy a를 사용하여 그들을 가져오세요:

intro cy a brings cy : Int and a : Nat into tactic state

다시 한 번, 당신은 그들의 구체적인 값을 가지지 않습니다. 왜냐하면 증명은 모든 가능한 값에 대해 작동해야 하기 때문입니다. 당신은 그들의 타입을 제외하고는 아무것도 모릅니다.

그 시점부터, 당신의 목표는 ↑a + birthYear cy a = cy이며, 이를 풀 수 있습니다:

theorem my_theorem : ∀ cy a, a + birthYear cy a = cy := by
  intro cy a
  unfold birthYear
  omega

∀ cy a가 본질적으로 cy와 a의 선언을 증명 "내부"로 이동시켰음을 주목하세요. 내부적으로, intro tactic은 cy와 a 인수를 가진 중첩된 함수를 생성하므로, 결국 이 theorem은 ∀를 추가하기 전과 같은 형태를 가집니다. Lean이 많은 스타일로 같은 것을 작성하게 해주는 것이 혼란스러울 수 있지만, 이것은 Lean 코어를 작게 유지하고 더 빠르게 진화하게 하며, tactic과 관례는 독립적으로 진화하고 프로젝트 간에 다를 수 있습니다.

∀를 사용하는 것이 이 예제에서 특히 매력적으로 보이지 않을 수 있지만, 익명 함수가 너무 많은 혼란을 추가할 중첩된 명제에 좋습니다. 또한 정리의 주장을 자신의 정의로 추출하는 것이 편할 수 있습니다:

def TheLawOfAging : Prop := ∀ cy a, a + birthYear cy a = cy
theorem my_theorem : TheLawOfAging := by
  unfold TheLawOfAging
  intro cy a
  unfold birthYear
  omega

Prop이 무엇인지 배우려면 제 이전 글을 확인하세요.

암시적 인수

이제 이 예제로 돌아가봅시다. 특히 이 라인:

def name := "Alice"
def birthYear (currentYear : Int) (age : Nat) :=
  currentYear - age
def main :=
  let year := birthYear 2025 42
  IO.println year

IO.println 위에 마우스를 올리면 깜짝 놀랄 수 있습니다: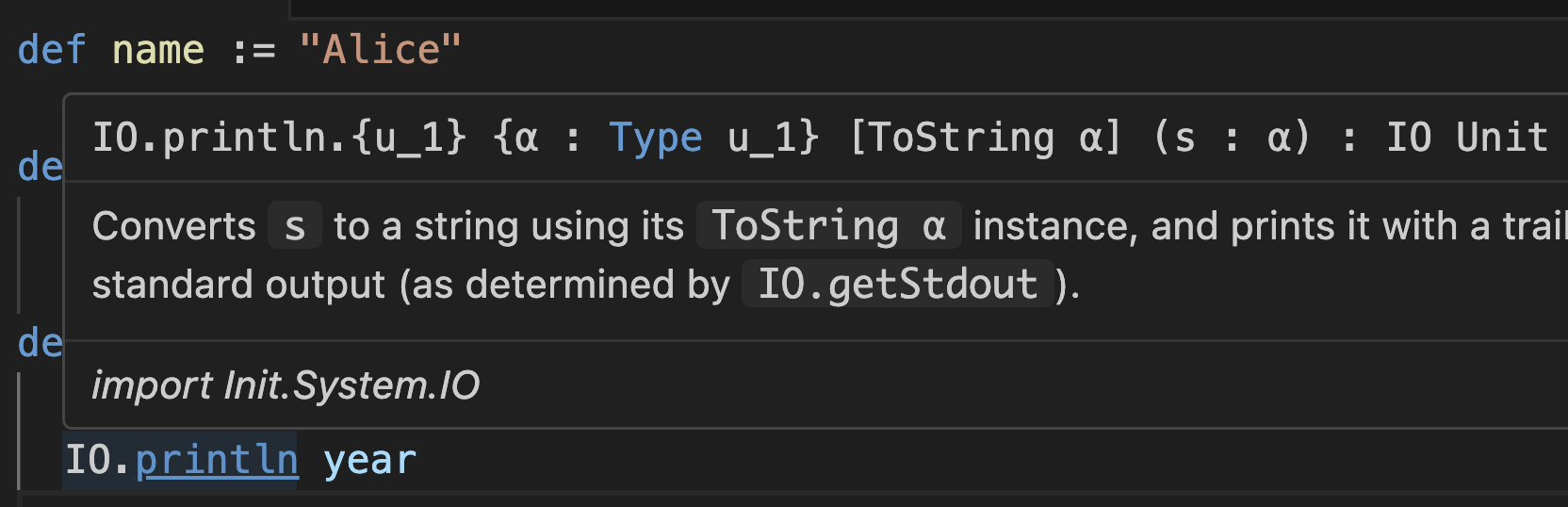

IO.println.{u_1} {a : Type u_1} [ToString α] (s: α) : IO Unit

이게 뭐죠?! 이 서명을 읽는 방법을 배우는 것은 Lean API를 이해하고 오류를 디버깅하는 능력을 엄청나게 향상시킬 것이므로, 대부분의 관련 주제를 논의하지 않았지만 분해하겠습니다.

핵심 통찰력은 { }와 [ ] 부분이 함수에 직접 전달하는 것이 아니라는 것입니다. 그래서 당신은 IO.println year를 작성할 수 있습니다. 하지만 이들은 실제 인수입니다 — 단지 Lean 자체가 채웁니다.

println을 Command+Click하여 {α}와 [ToString α]를 선언하는 것을 보세요:

def println {α} [ToString α] (s : α) : IO Unit :=
  print ((toString s).push '\n')

그래서 Lean이 당신을 위해 채운다면, 그들은 어디에서 오는 걸까요?

{ } 부분을 일반 암시적 매개변수라고 하며, 이미 전달된 매개변수를 기반으로 타입 추론으로 채워집니다. Lean이 명확하게 채울 수 없으면 불평하고 타입 검사를 통과하지 않을 것입니다. 여기서 α 인수는 암시적이지만, 당신이 명시적 (s : α) 인수로 전달한 것으로 결정됩니다. 당신은 Int를 출력하고 있으며, (s: Int)를 전달했으므로 α는 Int입니다. 이것은 제네릭과 유사하지만, Lean에서 제네릭은 단지 인수(종종 암시적)입니다.

[ToString α] 같은 [ ] 부분을 인스턴스 암시적 매개변수라고 하며, 지금까지 임포트한 코드에 따라 자동으로 채워집니다. Lean은 특정 인터페이스의 구현을 선언할 수 있게 하는 메커니즘을 가지고 있습니다 — 예를 들어, "Int와 Int를 빼는 방법" 또는 "Nat을 Int로 변환하는 방법" 또는 "Int를 String으로 바꾸는 방법". println 함수는 당신이 전달한 것(an Int)을 문자열로 바꾸는 방법을 알고 있는 ToString 구현을 원합니다. Lean은 코어에 ToString Int 구현을 가지고 있으므로, 그것이 println이 얻는 것입니다.

마지막으로, 맨 앞의 .{}는 이 함수의 타입이 사는 "우주"입니다. 이것은 거의 당신이 다루어야 할 것이 아니며, 자동으로 채워집니다.

암시적 및 인스턴스 인수는 수학적 객체와 증명 같은 복잡한 구조에서 작동할 때 엄청난 양의 보일러플레이트를 절약합니다. 하지만 여기서도, 그들은 Lean이 간단하고, 확장 가능하며, 강타입의 println API를 제공할 수 있게 해줍니다.

무엇이든 Command+Click하세요

더 많이 다루고 싶었지만 힘이 빠지고 있습니다 — 그리고 이 글은 이미 깁니다. 좋은 소식은 Lean이 매우 Command+Click 가능하기 때문에 당신이 직접 후드 아래를 엿볼 수 있다는 것입니다.

Nat과 String 같은 데이터 타입으로 Command+Click할 수 있으며, ∀ 같은 문법 조각도 마찬가지입니다. Lean의 대부분은 Lean 자체로 구현되어 있으며, 대부분의 경우 제가 발견한 것은 기대했던 것보다 더 간단하고 더 흥미로웠습니다.

/--
The natural numbers, starting at zero.
This type is special-cased by both the kernel and the compiler, and overridden with an efficient
implementation. Both use a fast arbitrary-precision arithmetic library (usually
[GMP](https://gmplib.org/)); at runtime, `Nat` values that are sufficiently small are unboxed.
-/
inductive Nat where
  /-- Zero, the smallest natural number. -/
  | zero : Nat
  /-- The successor of a natural number `n`. -/
  | succ (n : Nat) : Nat

누가 숫자가 단지 재귀적으로 생성된 열거형이라고 생각했을까요?

이런 재귀적으로 정의된 타입으로 구축된 언어가 원의 넓이가 π * r ^ 2라는 사실이나, 23명이 50% 이상의 같은 생일 확률을 초과하는 데 걸린다는 사실이나, 정육면체를 세제곱할 수 없다는 사실을 표현하고 증명할 수 있다는 것이 밝혀졌습니다. 하지만 당신은 또한 C로 컴파일되는 일반 프로그램을 작성할 수 있습니다. Async/await이 진행 중입니다.

아마도 당신은 중간에 뭔가를 만들 수 있을까요 — 증명과 얽힌 프로그램? Lean 코어 자체에서 이 패턴을 볼 수 있습니다: 여기 List.append (++) 함수가 있고, 여기 (as ++ bs).length = as.length + bs.length와 (as ++ bs) ++ cs = as ++ (bs ++ cs)의 증명이 있습니다. 다시 말해, 코드에서 Lean 데이터 구조를 사용하는 것은 또한 그 구조에 대한 알려진 사실을 재사용하여 당신의 자신의 코드에 대한 주장을 증명할 수 있게 해줍니다.

증명과 함께 프로그래밍하기

Lean은 오래된 아이디어와 많은 선행 작업을 기반으로 하지만, 새로운 것과 실용적인 것들이 있습니다. 때때로 저는 Go나 Haskell, Rocq나 C#, OCaml이나 Python을 작성하고 있는지 말할 수 없습니다. 그것의 신나는 무절제한 야망에서 그것은 Nemerle을 떠올리게 하지만, 또한 견고하고 기초가 있어 보입니다. 그것은 DeepMind와 Amazon을 포함한 산업과 학계에서 사용되고 있습니다. 프로그래밍 언어에 대해 흥분을 느낀 지 한참 되었습니다(마음에 두세요 — 순수 함수형 프로그래밍 언어).

어쨌든, 여기 증명과 함께 위아래로 세는 작은 프로그램이 있습니다.

def append (xs ys : List a) : List a := Id.run do
  let mut out := ys
  for x in xs.reverse do
    out := x :: out
  return out
theorem append_abcd : append ["a", "b"] ["c", "d"] = ["a", "b", "c", "d"] := by
  simp [append]
theorem append_length (xs ys : List a) : (append xs ys).length = xs.length + ys.length := by
  simp [append]
def count_up_and_down n :=
  let up := List.range (n)
  let down := (List.range (n + 1)).reverse
  append up down
theorem count_up_and_down_length n : (count_up_and_down n).length = n * 2 + 1 := by
  simp only [count_up_and_down, append_length, List.length_range, List.length_reverse]
  omega
def main := do
  IO.println "Enter a number: "
  let stdin ← IO.getStdin
  let input ← stdin.getLine
  let n := input.trim.toNat!
  let sequence := count_up_and_down n
  IO.println sequence

저는 이전에 증명과 함께 코드를 작성한 적이 없습니다. 당신은요?

Bluesky에서 논의하기 · Tangled에서 포크하기

아직 댓글이 없습니다.

첫 번째 댓글을 작성해보세요!