Boolean을 넘어서
overreacted 블로그 포스트 번역
2 + 2 = 4의 타입은 무엇일까요?TypeScript와 대부분의 다른 언어에서 논리 표현식은 Boolean 타입을 가집니다:
실제로 TypeScript가 이 모든 것이 논리 표현식이라는 것을 알 수 있으므로
: boolean 타입 주석을 생략할 수 있습니다: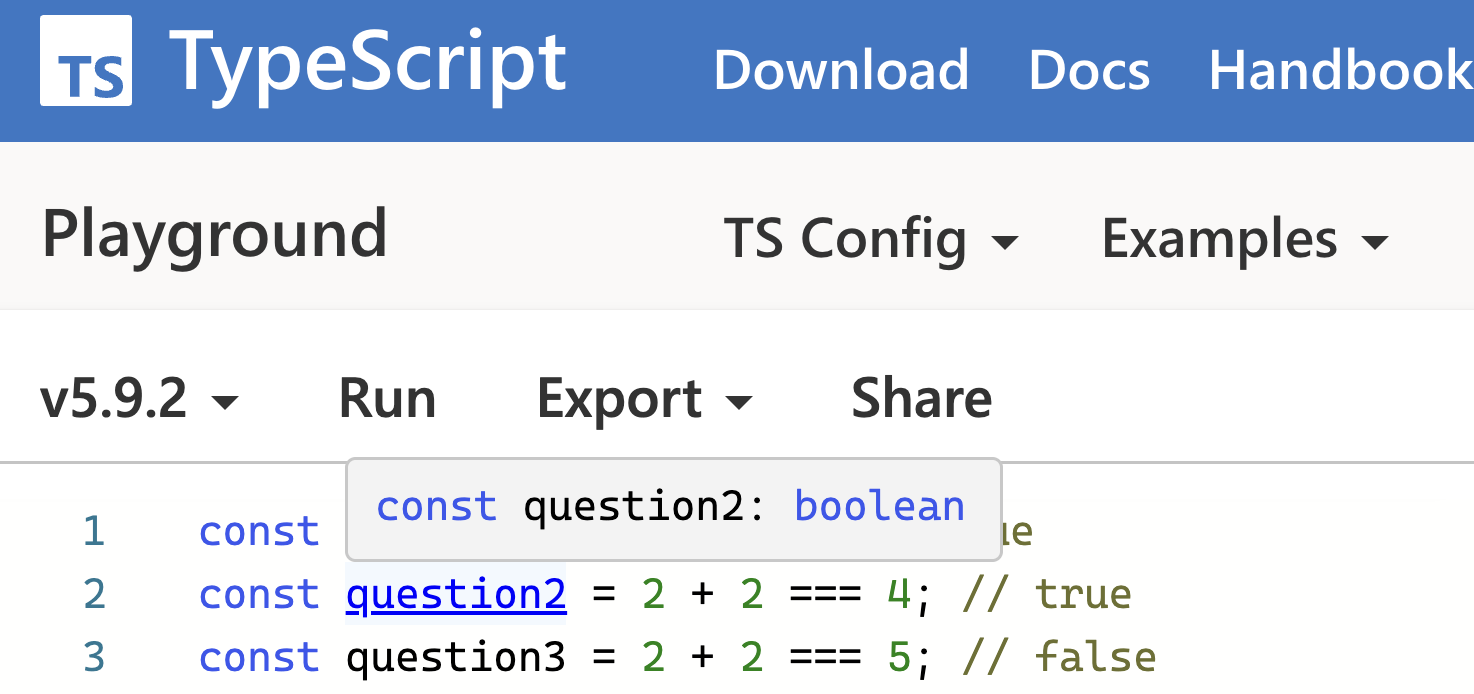
question1, question2, question3은 모두 같은 타입입니다. TypeScript에서는 하나의 boolean 타입만 있고, 그 타입의 값은 두 개뿐입니다(true와 false). 이를 시각화해봅시다(화살표는 "값이 타입입니다"를 의미합니다):
값으로서의 명제
Lean은 Boolean을 할 수 있지만, 기본적으로
2 + 2 = 4를 Boolean으로 보지 않습니다. 대신 Lean에서 2 + 2 = 4는 Prop을 줍니다 — "논리 명제"의 약자입니다:
2 + 2 = 4가 Prop 타입이라는 것을 기억하기 위해 명시적으로 주석을 달아봅시다:이제 이 값들과 타입들을 시각화해봅시다(화살표는 "값입니다"를 의미합니다):

이것은 다르게 보입니다!
TypeScript에서
2 + 2 === 4를 쓸 때, 그것은 즉시 어떤 boolean으로 "붕괴"됩니다(true 또는 false의 가능한 값 — 이 경우 true입니다).하지만 Lean에서
2 + 2 = 4를 쓸 때, 그것은 판정으로 "붕괴"되지 않습니다. 논리 명제 자체가 별개의 값입니다. 그것은 true 또는 false로 "변하지" 않습니다. 명제는 명제로 남습니다 — 추측적인 주장; 논리적 문장입니다.그렇다면 명제가 참인지 어떻게 알 수 있을까요?
계산하면 됩니다!
농담입니다.
Lean에서는 증명을 제시하여 컴퓨터를 설득해야 합니다. 흥미롭게도,
2 + 2 = 4는 값일 뿐만 아니라 또한 타입입니다. 증명은 그 타입의 값입니다.이를 풀어봅시다.
타입으로서의 명제
이 명제를 생각해봅시다:
2 = 2가 참이라고 컴퓨터를 설득하려면 어떻게 할까요? 프로그래머의 본능은 양쪽을 계산하고 비교하는 것일 수 있지만, Lean은 주로 수학자들이 사용하며, 수학은 계산의 영역을 훨씬 벗어납니다. 예를 들어, 1 + 1/2 + 1/4 + 1/8 + ... = 2를 증명하기 위해 "양쪽을 계산"하려고 하면, 프로그램은 무한한 시간과 무한한 메모리가 필요합니다.대신 Lean은 수학자처럼 생각하도록 강제합니다. 주장을 증명하려면 공리와 다른 증명을 기반으로 하고 이들을 논리적 논증으로 연결하는 증명을 제공해야 합니다. 증명을 구성하는 데 성공했다면, 주장을 증명한 것입니다.
이 주장에 대한 증명을 제공해봅시다:
지금은
by rfl이 정확히 무엇을 의미하는지 걱정하지 마세요; 나중에 다루겠습니다. foo = foo 같은 모든 명제를 증명할 수 있는 내장 Lean 값으로 생각하세요.하지만 타입을 봅시다! 앞의 예제처럼
2 = 2는 Prop 타입입니다. 하지만 여기 이상한 점이 있습니다: by rfl 자체는 claim1 타입입니다(2 = 2입니다).실제로
: claim1을 : 2 = 2로 바꾸면 여전히 타입 체크됩니다:이는 우리의 명제
2 = 2가 값일 뿐만 아니라 타입으로도 작동할 수 있다는 것을 의미합니다(by rfl은 정확히 2 = 2 타입의 값을 생성합니다):
TypeScript에서는 이런 "타입 타워"를 가질 수 없지만, Lean에서는 완전히 괜찮습니다.
by rfl 값은 2 = 2 타입을 가지고, 2 = 2는 Prop 타입을 가집니다.이제 이것이 의미하는 바를 봅시다.
우리가
2 = 2 타입의 어떤 값을 생성할 수 있었다는 사실은 우리가 그것을 증명했다는 것을 의미합니다. 명제를 증명하는 것은 그 타입의 값을 생성하는 것을 의미합니다. Lean에서 수학적 결과를 검증하는 것은 타입 체크 이상도 이하도 아닙니다.2 = 2와 2 + 2 = 4 타입의 값을 생성하는 데 성공했으므로(둘 다 by rfl로 할 수 있습니다), 이 명제들을 효과적으로 증명했습니다: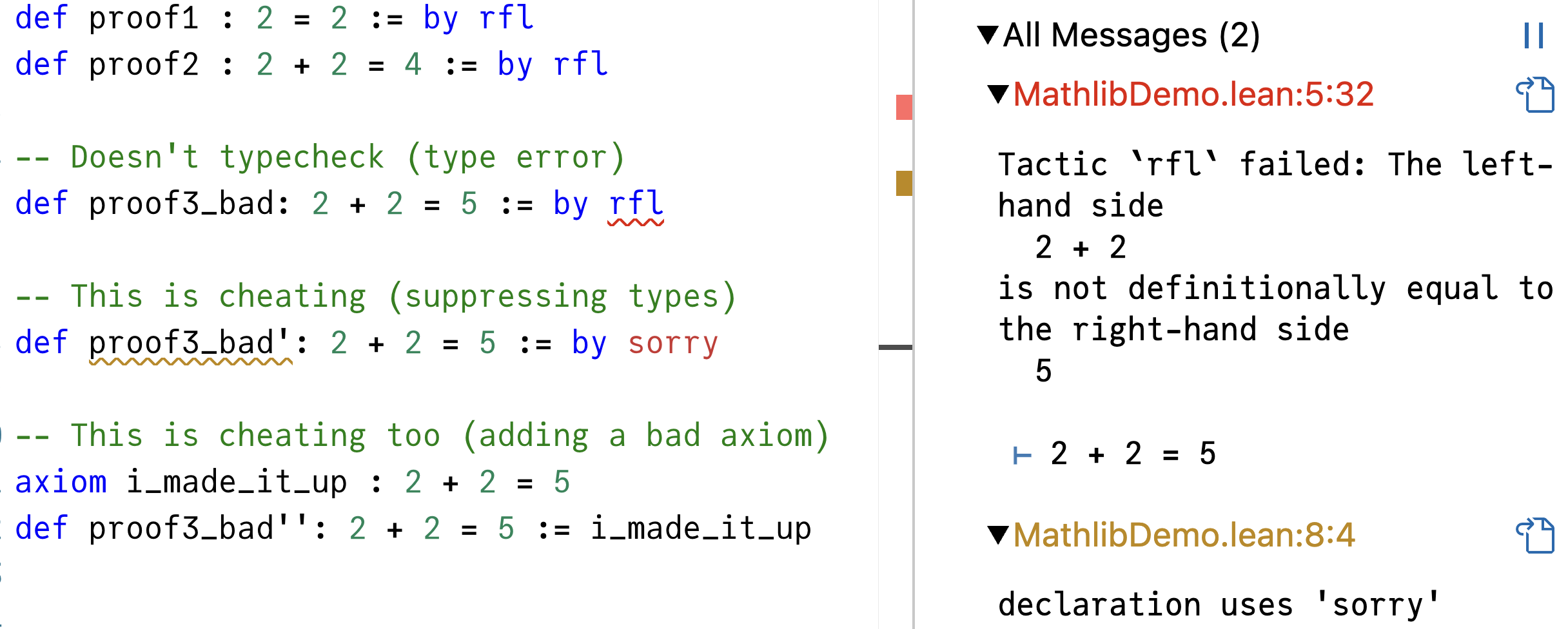
2 = 2와 2 + 2 = 4에 대한 증명을 찾았다는 사실을 시각화해봅시다:
2 = 2와 2 + 2 = 4와 달리, 2 + 2 = 5 타입은 "외로운" 상태입니다 — 우리는 그것에 대한 증명을 찾지 못했습니다. 명제가 거짓이라는 것이 무엇을 의미하는 걸까요?주의 깊은 독자는 우리가 실제로
2 + 2 = 5가 거짓이라는 것을 증명하지 않았다는 것을 알 수 있습니다. 그것이 참이고, 우리가 단지 운이 좋지 않아서 증명을 생성하지 못한 것은 아닐까요?다시 말해,
2 + 2 = 5가 증명 불가능하게 참인 것은 아닐까요?부정에 주목하세요
이것은 완전히 타당한 우려입니다!
우리가 할 수 있는 한 가지는 우리의 명제의 부정에 대한 증명을 찾는 것입니다:
2 + 2 = 5 앞의 Not에 주목하세요. Not (2 + 2 = 5)를 전체 별개의 명제로 생각할 수 있으며, 우리는 방금 그것에 대한 증명을 제공했습니다(by decide):
타입 체크됩니다, 따라서 우리는
Not (2 + 2 = 5)가 참이라는 것을 알 수 있습니다.by decide가 무엇을 하는지 궁금할 수 있습니다. 이전에 우리는 by rfl만 사용했습니다 — 하지만 그것은 foo = foo 같은 타입의 증명만 생성할 수 있습니다(예: 2 = 2). by rfl이 2 + 2 = 4를 해결할 수 있는 이유는 2 + 2와 4가 2, +, 4의 정의에 의해 양쪽에서 Nat.zero.succ.succ.succ.succ로 펼쳐지기 때문입니다. 따라서 2 + 2 = 4도 실제로 foo = foo 모양이므로 by rfl에 작동합니다.하지만
by rfl은 Not (foo = bar) 모양의 명제 증명을 생성할 수 없습니다. 이것이 우리가 더 강력한 by decide를 사용해야 하는 이유입니다. 이는 계산 가능한 모든 명제의 증명을 생성합니다. 수학 증명 중간에 계산기를 꺼내는 것과 같습니다. 2 + 2가 5가 아니라는 것을 "무심한" 논리적 변환으로 단계별로 증명하는 것은 가능하지만, 지루하므로 by decide가 우리를 위해 이를 수행합니다.중요한 부분은 타입 체크된다는 것입니다.
by rfl과 by decide 모두 단지 증명을 생성할 뿐입니다(나중에 증명이 무엇인지 볼 것입니다), 하지만 작은 Lean 커널이 실제 타입 체크를 수행합니다. 증명이 타입 체크되면, 논증은 반드시 올바릅니다.Not (2 + 2 = 5) 타입의 값을 생성했다는 사실은 Lean에서 2 + 2 = 5가 거짓이라고 말하는 것에 가장 가까운 것입니다. 그 증명은 우리의 공리가 이미 서로 모순되지 않고 Lean 커널에 버그가 없는 한, sorry 이외의 2 + 2 = 5 타입의 값을 찾지 못할 것이라는 것을 보장합니다:
그 의미에서,
2 + 2 = 5 같은 명제는 TypeScript의 never 타입과 유사합니다 — 그것은 속임수 없이 값을 생성하는 것이 불가능한 타입입니다.그리고 Lean에서, 그것이 명제가 거짓이라는 것을 의미합니다!
증명 무관성
주목할 가치가 있는 것은, 명제가 유효한 증명이 없을 수 있는 것처럼, 그것은 또한 많은 증명을 가질 수 있다는 것입니다 — 실제로 원하는 만큼 많이. 예를 들어,
2 + 2 = 4는 by rfl로 증명될 수 있지만, Mathlib의 기존 결과(편리하게 two_add_two_eq_four라고 불림)를 사용하거나, 더 강력한 by decide를 사용하여 증명될 수도 있습니다:위의 스니펫에서,
by decide, by rfl, two_add_two_eq_four를 통해 생성된 값들은 모두 같은 2 + 2 = 4 타입의 값입니다:
하지만 그들 사이에 초록색 등호 기호도 그렸습니다. Lean에서, 같은 명제의 모든 증명은 동등한 것으로 간주됩니다 — 일단 타입 체크되면, 다른 코드에는 구별할 수 없게 나타납니다. (원하면 증명할 수도 있습니다.)
그 의미에서, 각 명제는 최대 하나의 "별개의" 증명을 가집니다(찾았다면, 명제는 참입니다) 또는 증명이 없습니다(그러면 명제는 거짓이거나 증명 불가능하게 참입니다). 명제가 거짓이라는 것을 증명하고 싶다면, 그 부정의 증명을 찾아야 합니다. 그리고 공리에 모순이 포함되어 있다면, 모든 것이 증명 가능합니다.
타입화된 진실성
TypeScript 타입 시스템에서 논리가 어떻게 표현되는지 다시 봅시다:

이를 Lean에서 논리가 표현되는 방식과 비교해봅시다:

TypeScript 표현이 더 간단하지만(우리는 단일 타입의 두 값만 가집니다), 그것은 어떤 사실이 확립되었는지에 대한 지식을 지웁니다.
실제로 무엇을 의미할까요?
Lean은 주로 정리 증명보다는 계산에 사용되지만(따라서 사과 대 사과 비교가 아닙니다), Lean은 이 제약을 표현하기 쉽게 만듭니다. 우리가 해야 할 일은 함수가
x(a "실수", 또는 ℝ)를 취한다고 말하는 것입니다, x가 0보다 크거나 같다는 증명, 그리고 x가 1보다 작거나 같다는 증명:이제 이 함수를 호출하는 누구든지 이 두 증명도 제공해야 합니다.
0과 1 사이의 숫자 리터럴의 경우, by norm_num이 그러한 증명을 생성할 수 있습니다. 하지만 그 범위 밖의 숫자에 대한 증명을 생성할 수 없으므로, x를 1.2 또는 -1로 설정한 호출은 타입 체커에 실패합니다:
멋지지 않나요?
이를 "타입화된 진실성"으로 생각할 수 있습니다 — "
x가 0과 1 사이입니다"와 같은 사실이 한 곳에서 확실히 확립되고 프로그램 전체에서 안전하게 전달될 수 있습니다.증명 구성하기
중요하게도, 숫자 리터럴에 대한 사실 증명으로 제한되지 않습니다. 모든 공리와 기존 증명을 구성하고, 광범위한 결론을 내릴 수 있습니다.
예를 들어, 다른 값의 제곱 사인인
x를 가지고 있는 다른 수학적 정의를 작성하는 중이라고 가정해봅시다:그
x를 someFunction에 전달하고 싶지만, 이제 x가 0과 1 사이에 있다는 것을 증명해야 합니다. 문제는 0.99 또는 1.2 같은 구체적인 리터럴이 아니므로 정말로 그것이 무엇인지 알 수 없고, by norm_num은 더 이상 타입 체크되지 않습니다: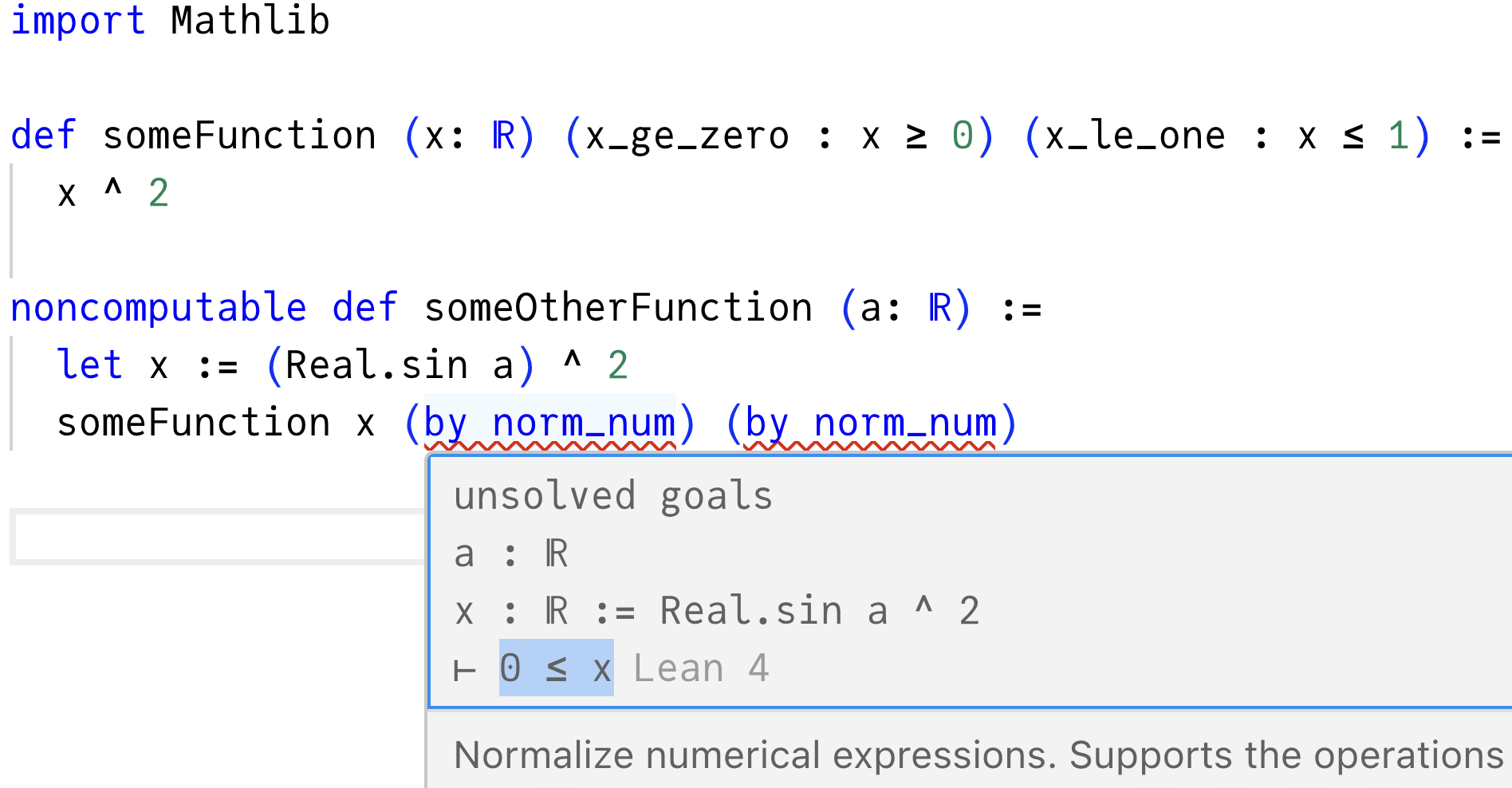
x ≥ 0과 x ≤ 1을 증명해야 합니다. 함수 호출 밖으로 이 명제들을 빼내서 작성하기 조금 더 편하게 해봅시다.시작하려면,
by sorry로 스텁하여 타입 체크되도록 합시다:이제 수학자의 모자를 쓸 수 있습니다. 실제로 이
x가 허용 가능한 범위 내에 있다고 믿을 좋은 이유가 있습니다. 그것은 제곱이므로 음이 아니어야 합니다. 그리고 그것은 사인의 제곱이며, 사인 자체는 -1과 1 사이에 머물러 있습니다.Lean이 Mathlib에서 정확히 필요한 증명을 찾을 수 있는지
apply?를 작성하여 확인할 수 있습니다(물음표는 그것이 대화형 도구이고 커밋되지 않아야 함을 의미합니다).실제로 일치하는 것이 있습니다:
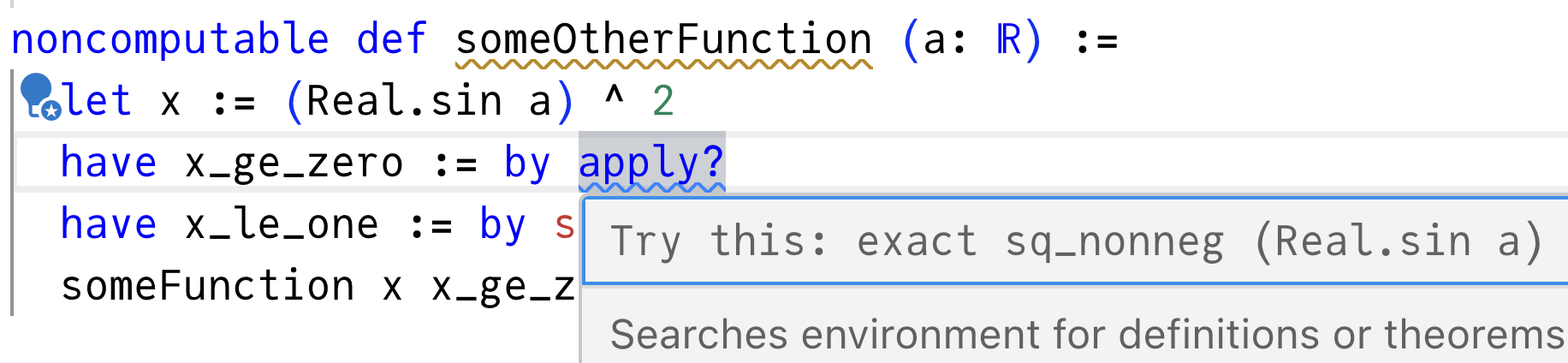
Lean은 Mathlib 라이브러리에서
sq_nonneg라는 기존 증명을 찾았다고 말합니다. 이는 foo ^ 2 ≥ 0 모양의 모든 명제의 증명이므로, sin a에 적용하여 (sin a) ^ 2 ≥ 0의 증명을 생성할 수 있습니다.sin a를 sq_nonneg에 exact sq_nonneg (Real.sin a)로 전달할 수 있습니다:또는
apply sq_nonneg를 사용하고 Lean이 타입으로부터 인수를 추론하도록 할 수 있습니다:이제 첫 번째 증명이 타입 체크되므로, 두 번째 증명으로 운을 시도해봅시다:
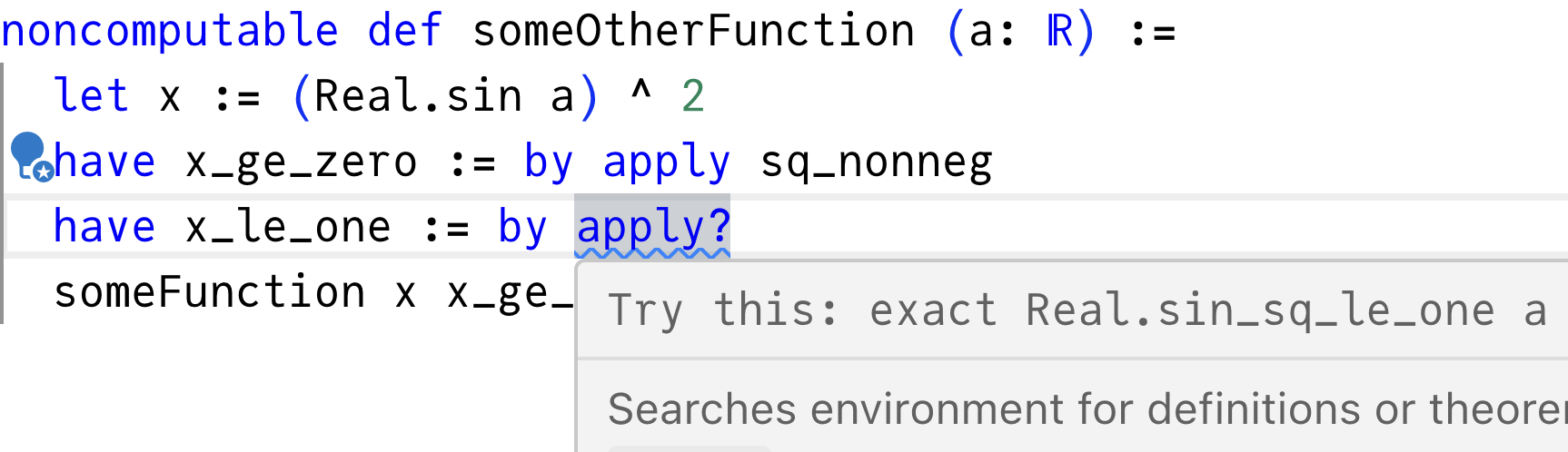
또 다른 일치! Mathlib은 우연히
sin_sq_le_one("사인 제곱은 1보다 작음")이라는 증명을 포함하고 있으며, 이는 정확히 필요한 것입니다. (sin foo) ^ 2 ≤ 1 모양의 명제를 증명하고, (sin a) ^ 2 ≤ 1이 필요합니다. exact sin_sq_le_one a처럼 a를 명시적으로 전달하거나, apply가 인수를 추론하도록 할 수 있습니다:이제 전체가 타입 체크됩니다!

Mathlib에서 정확히 필요한 증명을 찾을 수 있을 때마다 운이 좋은 것은 아니지만, 그것이 요점이 아닙니다. Mathlib은 단지 오픈 소스 증명의 모음입니다. Lean은 그러한 증명을 표현하고 검증하고 구성하는 언어를 제공합니다.
보시다시피, Lean은 특정 숫자 리터럴에 대해 "똑똑한" 것으로 제한되지 않습니다 — 또는 계산될 수 있는 것들도 아닙니다. 실제로 이 예제에서, 나는
someOtherFunction을 noncomputable로 표시해야 했습니다. 왜냐하면 그것은 Mathlib에서 noncomputable인 Real.sin을 사용하기 때문입니다. 컴퓨터에서 무한 정밀도로 실수의 사인을 안정적으로 계산하는 것은 불가능하지만, 수학은 "실수의 사인"과 같은 개념을 정확하게 이야기해야 합니다. Lean은 계산될 수 없는 개념에 대한 명제의 증명을 구성할 수 있게 합니다 — 숫자 π, 무한 급수, 무한 집합 등 — 그리고 그들에 대한 사실을 엄격하게 증명합니다.by 뒤에
남아있는 큰 미스터리가 하나 있습니다 — 증명이 무엇인가?
by는 무엇을 하나요?기본으로 돌아가봅시다:
2 = 2는 정확히 무엇일까요? VS Code에서 Command+Click하면, a = b가 실제로 어떤 Eq a b에 대한 문법 설탕으로 정의되어 있다는 것을 알 수 있습니다: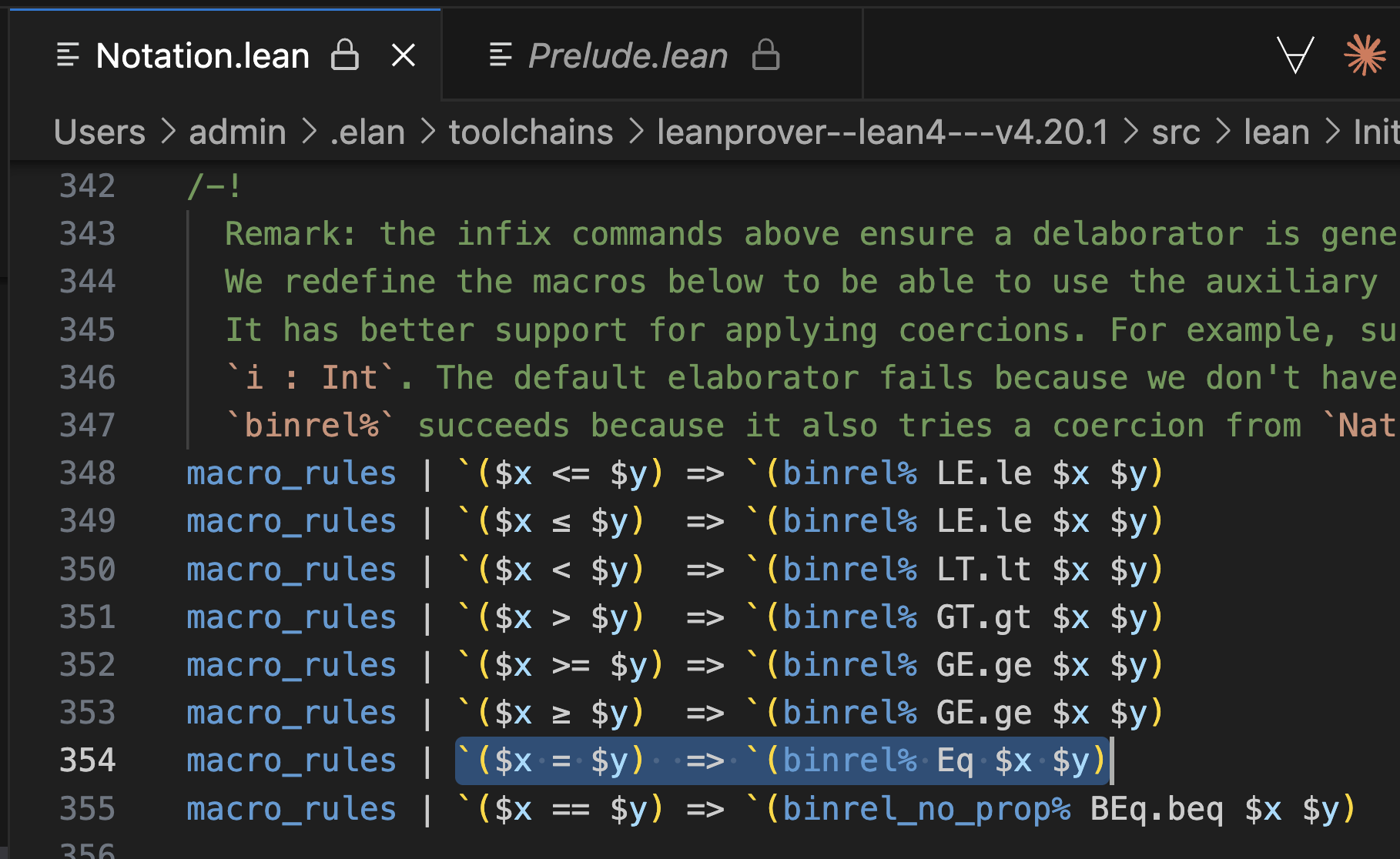
(네, Lean 기초의 많은 부분이 실제로 Lean으로 작성되어 있습니다.)
다시 말해,
2 = 2는 실제로 2와 2를 가진 Eq에 대한 함수 호출입니다:좋습니다, 하지만
Eq는 무엇일까요? VS Code에서 Command+Click하면, Eq가 함수와 타입 사이의 하이브리드로 Lean에서 정의된 타입이라는 것을 알 수 있습니다:이것은 좀 밀도가 높습니다! 이 문법이 TypeScript로 어떻게 변환되는지 봅시다? 이것은 실제 TypeScript가 아니고 타입 체크되지 않지만, 내 마음에는 이렇게 읽습니다:
Lean 디자이너들이 목표로 하는 것은
Eq<X, X> 같은 타입의 값만 생성할 수 있도록 보장하는 것입니다. 예를 들어, Eq.refl(2)는 Eq<2, 2> 타입의 값을 주고, Eq.refl("hi")는 Eq<"hi", "hi"> 타입의 값을 주지만, Eq<2, 3> 타입의 값을 구성하는 것은 불가능합니다."
Eq<2, 3> 타입의 값을 생성하는 것이 불가능해야 한다"는 것은 "2 = 3을 증명하는 것이 불가능해야 한다"와 의심스럽게 유사합니다. 프로그래밍과 수학을 함께 연결하는 방법 — 증명의 개념을 타입으로 표현하는 방법을 찾은 것처럼 느껴집니다. (아마도 우리가 처음은 아닐 것입니다.)이제 Lean과 어떻게 연결되는지 봅시다.
먼저, 표기법 경고 — Lean은 "제네릭"의 개념이 없습니다(
<> 같은 문법도 없습니다) 왜냐하면 불필요하기 때문입니다. Lean에서 타입은 값이므로, 제네릭은 단지 함수 인수입니다(종종 선택적이고 추론됨). 따라서 Eq<2, 2> 대신 Eq 2 2를 쓸 것입니다. 네, 그것은 타입을 반환하는 함수 호출입니다. (그것을 먹어라, TypeScript!)따라서
Eq<2, 2>를 Eq 2 2(타입)로, Eq.refl(2)를 Eq.refl 2로 쓸 것입니다.이제 우리의 친구
by rfl을 기억해봅시다:그것은 단지
Eq.refl에 대한 호출을 생성하는 매크로(또는 Lean 용어로 tactic)입니다:이를 다시 함께 놓아봅시다:
by rfl tactic은 Eq.refl 2 증명을 생성하며, 이는 Eq 2 2 타입입니다(또는 더 좋은 2 = 2), 그 자체는 Prop 타입의 값입니다. 타입이 통과하므로, 증명됩니다:
반면에,
2 = 3을 증명하려고 시도했다면, 어떻게든 Eq 2 3 타입의 값을 구성해야 합니다. 하지만 그것은 불가능합니다. Eq 타입의 유일한 생성자는 Eq.refl이고, 그것은 Eq 2 2, Eq 3 3 등의 타입의 값만 생성할 수 있습니다 — 왼쪽이 오른쪽 인 경우입니다.이제 전체 그림을 볼 수 있습니다:

P.S.
0
5
댓글
?
아직 댓글이 없습니다.
첫 번째 댓글을 작성해보세요!
Inkyu Oh님의 다른 글
더보기
번역
RSC가 번들러와 통합되는 이유
Inkyu Oh • Front-End
0
0
16
Lean 문법 입문서
Inkyu Oh • AI & ML-ops
0
0
9

어떤 버그든 고치는 방법
Inkyu Oh • Front-End
0
0
18

번역
실제로 작동하는 간단한 검색 엔진 만들기
Inkyu Oh • Back-End
1
0
22