[번역] 객체 배열(SoA 패턴)이 인터리브 배열을 이기는 이유: JavaScript 성능의 심연
Royal Bhati - 2025-12-23
지난주에 Go 언어의 메모리 정렬(Memory alignment)에 대해 읽다가 JavaScript에서도 비슷한 개념을 탐구해보고 싶다는 생각이 들었습니다. 저는 AoS와 SoA 패턴(자세한 내용은 아래 참고)을 사용하여 100만 개의 3D 포인트에 대한 x, y, z 좌표를 합산하는 루프를 작성했고, 두 방식 사이에서 4배의 성능 차이를 발견했습니다. SoA가 더 나은 성능을 보일 것이라는 점은 알고 있었지만, 이처럼 단순한 프로그램에서 4배나 차이가 날 줄은 예상하지 못했습니다.
처음에는 단순히 TypedArray가 "더 빠르기" 때문이라고 생각했습니다. 하지만 더 깊이 파고든 결과, 그 이면에는 더 미묘한 이야기가 숨어 있다는 것을 깨달았습니다. 이 포스트는 제가 배운 내용에 관한 것입니다.
벤치마크
저는 100만 개의 3D 포인트를 저장하는 두 가지 방법을 비교했습니다.
객체 배열 (Array of Objects, AoS 패턴):
데이터가 객체 단위로 저장되므로, 각 요소는 모든 필드를 함께 포함합니다.
const points = [];for (let i = 0; i < N; i++) { points.push({ x: Math.random(), y: Math.random(), z: Math.random() });}let sum = 0;for (let i = 0; i < N; i++) { sum += points[i].x + points[i].y + points[i].z;}TypedArray의 객체 (Object of TypedArrays, SoA 패턴):
데이터가 필드 단위로 저장되므로, 각 배열은 모든 요소에 대한 하나의 속성만 보유합니다.
const points = { x: new Float64Array(N), y: new Float64Array(N), z: new Float64Array(N)};for (let i = 0; i < N; i++) { points.x[i] = Math.random(); points.y[i] = Math.random(); points.z[i] = Math.random();}let sum = 0;for (let i = 0; i < N; i++) { sum += points.x[i] + points.y[i] + points.z[i];}N = 1,000,000일 때 결과:
접근 방식 | 시간 |
|---|---|
객체 배열 (AoS) | ~42ms |
TypedArray의 객체 (SoA) | ~10ms |
4배 더 빠릅니다. 하지만 여기서 중요한 점은 이것이 단순히 일반 배열(Array) 대 TypedArray의 대결이 아니라는 것입니다. 실제로는 여러 요소가 동시에 변하고 있으며, 각각을 이해하는 것이 중요합니다.
JavaScript에서의 TypedArray vs 일반 배열
컴퓨터 과학(CS) 배경지식만 있거나 C, C++, Go와 같은 강타입 언어의 경험만 있는 상태에서 JavaScript를 처음 접한다면, JS의
Array 또한 연속된 메모리 블록을 제공할 것이라고 자연스럽게 가정할 수 있습니다.하지만 그렇지 않습니다!!! 네, 제대로 읽으신 게 맞습니다.
V8 엔진은 이를 다음과 유사한 형태로 저장합니다.
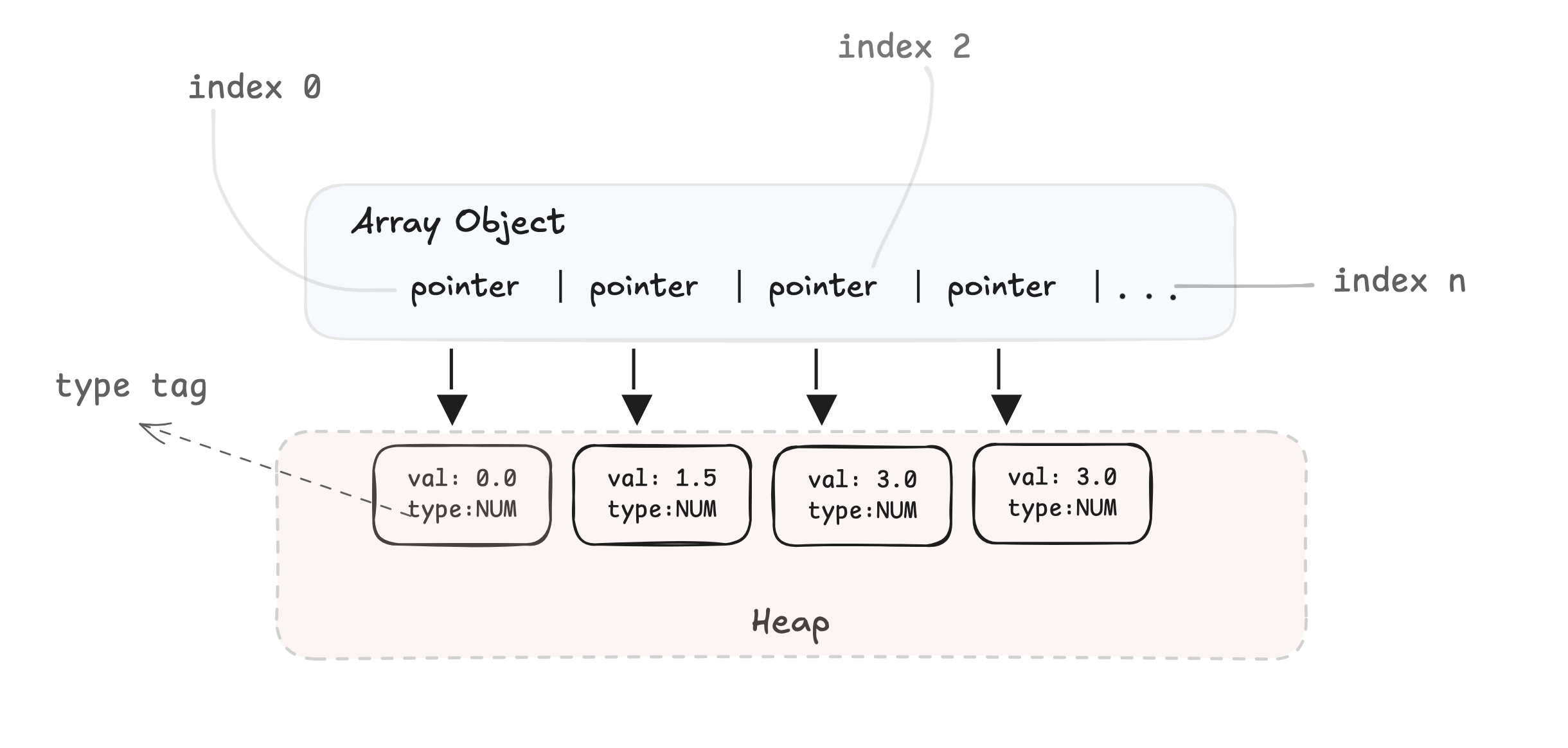
모든 접근은 다음을 의미합니다:
- 배열에서 포인터 로드
- 포인터를 따라 힙(Heap) 객체로 이동
- 타입 태그 확인 (이게 정말 숫자인가?)
- 부동 소수점(Float) 값 추출
- 이제 수학 연산 수행
반복문 한 번마다 할 일이 너무 많습니다. 그런데 왜 이런 방식으로 저장되는 걸까요?
JS 배열은 유연성이라는 저주에 걸려 있기 때문에, JS 개발자가 다음과 같은 코드를 작성하는 것을 막을 방법이 없기 때문입니다.
arr[500000] = "보세요, 숫자 배열에 문자열이 들어왔어요";arr[999999] = { look: "ma", an:"object", in:"numeric array" };arr.length = 5; // 보세요, 다 날려버렸어요delete arr[42]; // 보세요, 구멍(hole)을 만들었어요하지만 잠깐만요 — 모든 요소가 숫자인 숫자 배열의 경우에는 이야기가 다릅니다.
V8은 배열에 무엇이 들어있는지 추적하는 정교한 "요소 종류(Element kinds)"를 가지고 있습니다. 다음과 같이 작성하면:
const arr = new Array(1000000);for (let i = 0; i < arr.length; i++) { arr[i] = i * 1.5;}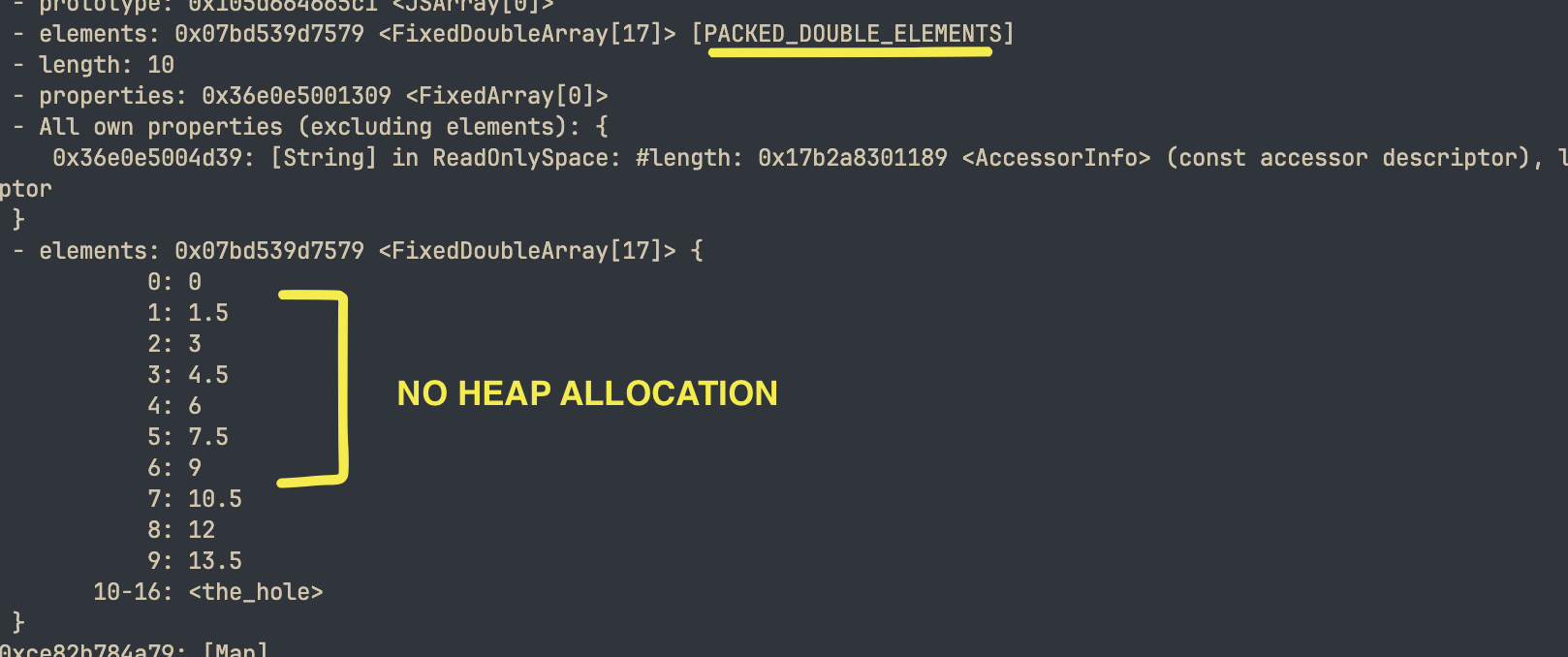
V8은 당신이 double(배정밀도 부동 소수점)만 저장하고 있다는 것을 감지하고
PACKED_DOUBLE_ELEMENTS를 사용합니다. 이는 힙 포인터가 아닌, 박싱되지 않은(Unboxed) 64비트 부동 소수점의 연속된 배열입니다. C 배열과 똑같이 메모리에 나란히 놓인 순수 IEEE 754 double 값들입니다.- 이제 항상 float64이므로 타입 체크가 필요 없습니다.
- 길이가 고정되어 루프 밖에서 경계 검사(Bounds checks)가 이루어집니다.
- 관리할 포인터가 없습니다.
- 때로는 SIMD까지 활용될 수 있습니다.
"접근할 때마다 포인터를 추적한다"는 이야기는 혼합된 타입이 있거나 희소 배열(Sparse array)인 경우에만 해당됩니다.
const arr = [];for (let i = 0; i < 10; i++){ arr.push(i * 1.5); if(i === 5){ arr[i] = "보세요, 숫자 배열에 문자열이 들어왔어요"; } if(i === 7){ arr[i] = { look: "ma", an:"object", in:"numeric array" }; }}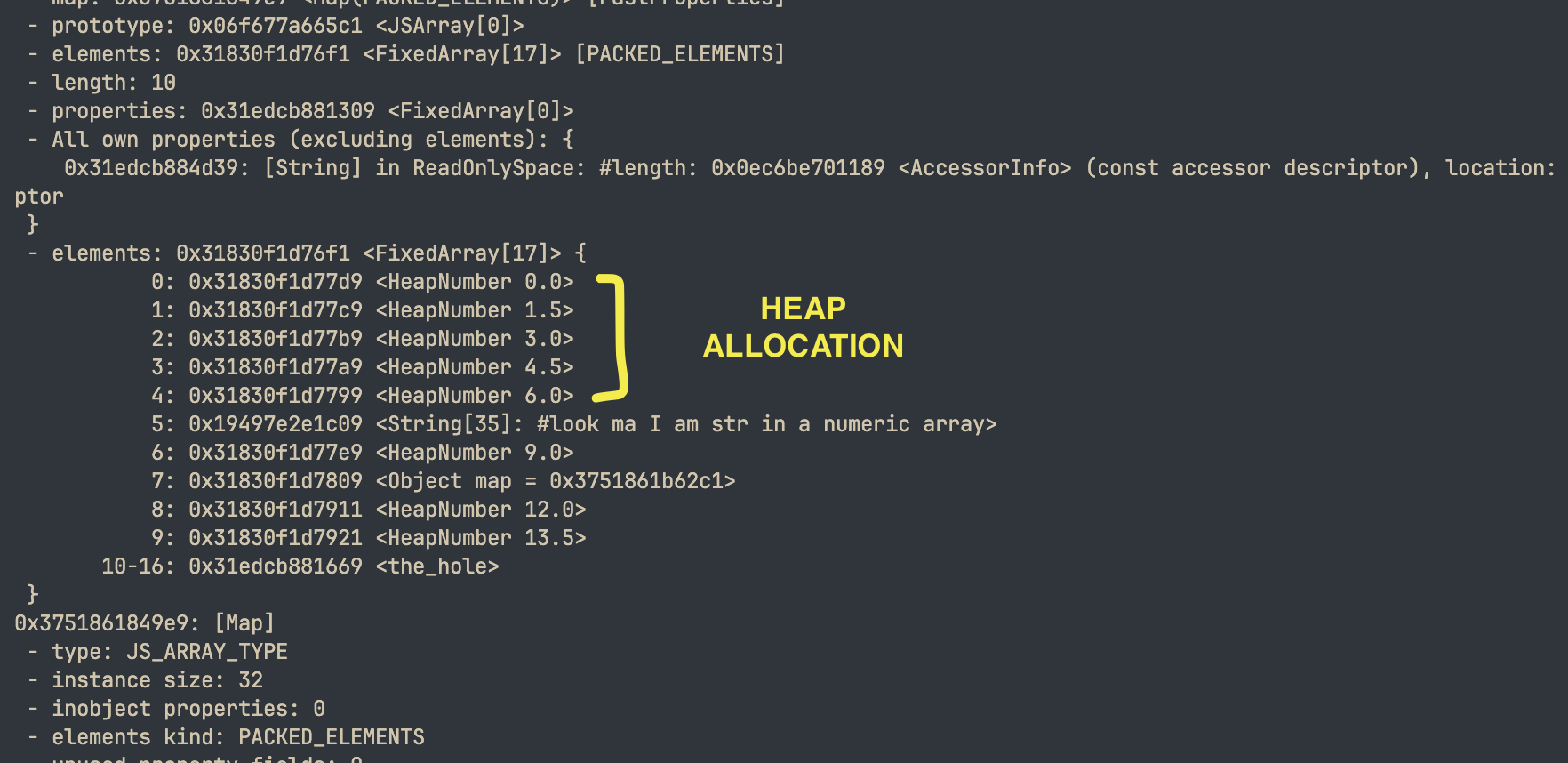
TypedArray 효과 확인하기
이 결과가 실제 정답에 큰 기여를 하지는 않겠지만, TypedArray 단독으로 얼마나 기여하는지 확인해보고 싶었습니다.
const N = 1_000_000;const regular = [];for (let i = 0; i < N; i++) regular.push(Math.random());const typed = new Float64Array(N);for (let i = 0; i < N; i++) typed[i] = Math.random();function sumRegular() { let sum = 0; for (let i = 0; i < regular.length; i++) sum += regular[i]; return sum;}function sumTyped() { let sum = 0; for (let i = 0; i < typed.length; i++) sum += typed[i]; return sum;}
잘 최적화된 일반 배열과 TypedArray 사이의 차이는 무시할 수 있는 수준이었으며, 때로는 오차 범위 내에 있었습니다. TypedArray의 장점은 성능을 더 높이는 것이라기보다, 조건이 이상적일 때 얻을 수 있는 그 성능을 "보장"하는 것에 가깝습니다.
속도 향상의 실제 요인
제 벤치마크는 다음을 비교하고 있었습니다.
- 객체 vs 원시 타입(Primitives) —
point.x는 속성 조회가 필요하지만,arr[i]는 직접 인덱싱입니다.
- AoS vs SoA 레이아웃 — 구조체 배열(Array-of-Structures) 대 배열 구조체(Structure-of-Arrays).
이를 분석해 보겠습니다.
요인 1: 속성 접근 오버헤드
모든
points[i].x는 다음을 요구합니다:- 객체를 가져오기 위해 배열 인덱싱
- 객체의 숨겨진 클래스(Hidden class)에서 속성 "x" 조회
- 값 반환
반면
points.x[i]는:- "x"를 한 번 조회 (JIT에 의해 루프 밖으로 끌어올려짐(Hoisted))
- 직접적인 배열 인덱싱
V8이 최적화하더라도 속성 조회 비용은 공짜가 아닙니다.
요인 2: 객체 할당 및 메모리 레이아웃
100만 개의 객체는 100만 개의 별도 힙 할당을 의미합니다. 각 객체가 작더라도 다음과 같은 문제가 발생합니다:
- 메모리 파편화(Fragmentation)
- 나쁜 캐시 지역성(Cache locality) (객체들이 연속적으로 배치된다는 보장이 없음)
- 수많은 객체를 추적해야 하는 가비지 컬렉션(GC) 압박
세 개의 TypedArray를 사용하는 SoA 패턴은 정확히 세 번의 할당만 발생하며, 각각 연속된 메모리를 보장받습니다.
수정 사항 (2025/12/29)
Reddit의 누군가가 이 학습 내용에 대해 따끔한 한마디를 남겼습니다:
첫 번째 AoS 방식은 배열을 생성하고 루프의 각 반복마다 요소를 push합니다. 반면 SoA는 초기화 시점에 필요한 크기의 배열을 생성한 다음 배열 인덱스를 사용하여 효율적으로 기록합니다. 이것이 당신이 보고 있는 속도 향상의 대부분을 차지할 것입니다. 이 테스트는 조작된 문제이고, 어리석은 전제이며, 잘못된 테스트 케이스이고, 솔직히 무지한 게 아니라면 부정직한 것입니다.
일리가 있는 지적입니다.
push() 대 사전 할당(Pre-allocation)이 실제로 읽기(READ) 성능에 영향을 미치는지 테스트해 보겠습니다. push()와 사전 할당으로 생성된 메모리 레이아웃이 다를 수 있기 때문입니다. (생성 루프가 아닌 합산 루프의 시간만 측정하므로 읽기 성능만 측정합니다.)const N = 1_000_000;const ITERATIONS = 100;const aosPush = [];for (let i = 0; i < N; i++) { aosPush.push({ x: Math.random(), y: Math.random(), z: Math.random() });}const aosPrealloc = new Array(N);for (let i = 0; i < N; i++) { aosPrealloc[i] = { x: Math.random(), y: Math.random(), z: Math.random() };}function Point(x, y, z) { this.x = x; this.y = y; this.z = z; }const aosConstructor = new Array(N);for (let i = 0; i < N; i++) { aosConstructor[i] = new Point(Math.random(), Math.random(), Math.random());}const soaTyped = { x: new Float64Array(N), y: new Float64Array(N), z: new Float64Array(N)};for (let i = 0; i < N; i++) { soaTyped.x[i] = Math.random(); soaTyped.y[i] = Math.random(); soaTyped.z[i] = Math.random();}const soaRegular = { x: new Array(N), y: new Array(N), z: new Array(N)};for (let i = 0; i < N; i++) { soaRegular.x[i] = Math.random(); soaRegular.y[i] = Math.random(); soaRegular.z[i] = Math.random();}function benchmark(name, fn) { for (let i = 0; i < 10; i++) fn(); const times = []; for (let i = 0; i < ITERATIONS; i++) { const start = performance.now(); fn(); times.push(performance.now() - start); } times.sort((a, b) => a - b); console.log(`${name}: ${times[Math.floor(times.length / 2)].toFixed(3)}ms`);}console.log('AoS 변형 (모두 객체 읽기):');benchmark(' AoS (push)', () => { let sum = 0; for (let i = 0; i < N; i++) sum += aosPush[i].x + aosPush[i].y + aosPush[i].z; return sum;});benchmark(' AoS (사전 할당)', () => { let sum = 0; for (let i = 0; i < N; i++) sum += aosPrealloc[i].x + aosPrealloc[i].y + aosPrealloc[i].z; return sum;});benchmark(' AoS (생성자)', () => { let sum = 0; for (let i = 0; i < N; i++) sum += aosConstructor[i].x + aosConstructor[i].y + aosConstructor[i].z; return sum;});console.log('\nSoA 변형 (객체 없음):');benchmark(' SoA (TypedArray)', () => { let sum = 0; for (let i = 0; i < N; i++) sum += soaTyped.x[i] + soaTyped.y[i] + soaTyped.z[i]; return sum;});benchmark(' SoA (일반 Array)', () => { let sum = 0; for (let i = 0; i < N; i++) sum += soaRegular.x[i] + soaRegular.y[i] + soaRegular.z[i]; return sum;});결과:
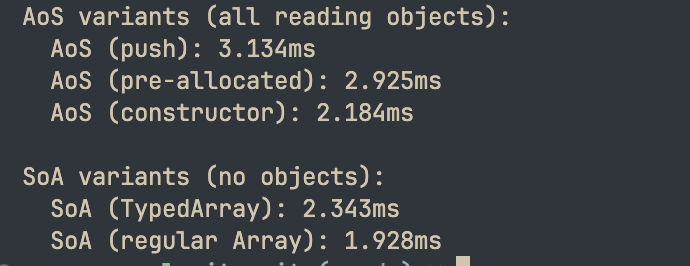
보시다시피
push() 대 사전 할당은 거의 차이가 없습니다.SoA의 캐시 친화성에 대하여
생각해 보기 전까지는 완전히 깨닫지 못했던 사실이 있습니다. 바로 메모리 레이아웃이 캐시 동작을 결정한다는 것입니다.
CPU 캐시는 캐시 라인(보통 64바이트) 단위로 작동합니다. 우리가
arr[i]를 읽을 때, CPU는 해당 주소를 포함하는 전체 라인을 가져옵니다. 데이터가 연속적이라면, 그 한 번의 가져오기로 8개의 float 값을 공짜로 얻는 셈입니다. 데이터가 힙 객체로 흩어져 있다면, 캐시 라인의 대부분은 필요 없는 쓰레기 데이터가 됩니다.프리페처(Prefetcher) 또한 TypedArray를 좋아합니다. 순차적 접근 패턴인가요? 그러면 당신이 요청하기도 전에 다음 캐시 라인을 가져오기 시작할 것입니다.
하지만 세 개의 별도 배열을 사용하는 제 SoA 벤치마크에는 미묘한 고려 사항이 있습니다.
sum += points.x[i] + points.y[i] + points.z[i];이 코드는 반복당 세 개의 서로 다른 메모리 영역을 건드립니다. N이 매우 크면 세 배열을 동시에 L1 캐시에 담지 못할 수도 있고, 잠재적으로 캐시 압박을 유발할 수 있습니다.
그래서 더 나은 성능을 얻는 방법을 찾아보았습니다. 인터리브(Interleaved) TypedArray가 이 특정 접근 패턴에 대해 더 나은 지역성을 가질 수 있습니다.
// 인터리브 방식: x0, y0, z0, x1, y1, z1, ...const points = new Float64Array(N * 3);이렇게 하면 각 포인트의 x, y, z가 동일한 캐시 라인에 유지됩니다. 최적의 레이아웃은 접근 패턴에 따라 다릅니다. SoA는 한 번에 하나의 컴포넌트만 처리할 때 빛을 발하고, 인터리브 방식은 항상 모든 컴포넌트가 함께 필요할 때 더 잘 작동합니다.
호기심이 생겨서 얼마나 성능 향상이 있는지 테스트해 보기로 했습니다.
인터리브 패턴 테스트
const N = 1_000_000;const ITERATIONS = 100;const soA = { x: new Float64Array(N), y: new Float64Array(N), z: new Float64Array(N)};for (let i = 0; i < N; i++) { soA.x[i] = Math.random(); soA.y[i] = Math.random(); soA.z[i] = Math.random();}const interleaved = new Float64Array(N * 3);for (let i = 0; i < N; i++) { interleaved[i * 3] = Math.random(); interleaved[i * 3 + 1] = Math.random(); interleaved[i * 3 + 2] = Math.random();}function benchmark(name, fn) { for (let i = 0; i < 10; i++) fn(); const times = []; for (let i = 0; i < ITERATIONS; i++) { const start = performance.now(); fn(); times.push(performance.now() - start); } times.sort((a, b) => a - b); console.log(`${name}: ${times[Math.floor(times.length / 2)].toFixed(3)}ms`); return times[Math.floor(times.length / 2)];}const soaTime = benchmark('SoA (3개의 TypedArray)', () => { let sum = 0; for (let i = 0; i < N; i++) { sum += soA.x[i] + soA.y[i] + soA.z[i]; } return sum;});const interleavedTime = benchmark('인터리브 TypedArray', () => { let sum = 0; for (let i = 0; i < N * 3; i += 3) { sum += interleaved[i] + interleaved[i + 1] + interleaved[i + 2]; } return sum;});결과:

잠깐, SoA가 여전히 인터리브보다 빠르다고요? 이건 제 캐시 지역성 이론과 상충됩니다.
변수 격리 테스트
동일한 데이터에 대해 순수 접근 패턴만 테스트하여 변수를 격리해 보겠습니다.
const N = 1_000_000;const data = new Float64Array(N * 3);for (let i = 0; i < N * 3; i++) data[i] = Math.random();// 반복당 3번의 먼 거리 접근function threeDistantAccesses() { let sum = 0; for (let i = 0; i < N; i++) { sum += data[i] + data[i + N] + data[i + N * 2]; } return sum;}// 반복당 1번의 순수 순차 접근function pureSequential() { let sum = 0; for (let i = 0; i < N * 3; i++) { sum += data[i]; } return sum;}// 반복당 3개씩 그룹화된 순차 접근function groupedSequential() { let sum = 0; for (let i = 0; i < N * 3; i += 3) { sum += data[i] + data[i + 1] + data[i + 2]; } return sum;}결과:

순수 순차 접근이 가장 느리다고요?! 완벽한 캐시 지역성을 가졌음에도 불구하고 그룹화된 접근보다 거의 2배 느립니다.
한 가지 잠재적 해답: 루프 오버헤드
지배적인 요인은 캐시 지역성이 아니라 루프 오버헤드였습니다.
각 반복에는 고정된 비용이 발생합니다:
- 카운터 증가
- 길이와 비교
- 분기 예측(Branch prediction)
- 루프 관리 작업
반복당 더 많은 작업을 수행하면 이 비용을 분산(Amortize)시킬 수 있습니다.
// 3,000,000번 반복, 각 1번의 덧셈 — 루프 오버헤드를 300만 번 지불for (let i = 0; i < N * 3; i++) { sum += data[i];}// 1,000,000번 반복, 각 3번의 덧셈 — 루프 오버헤드를 100만 번 지불for (let i = 0; i < N * 3; i += 3) { sum += data[i] + data[i+1] + data[i+2];}두 번째 버전은 총 작업량은 같지만 루프 오버헤드를 3배 적게 지불합니다.
또한 현대의 CPU는 여러 덧셈을 병렬로 실행할 수 있습니다(명령어 수준 병렬성, ILP).
a + b + c는 CPU 파이프라인에서 부분적으로 겹쳐서 실행될 수 있지만, 이는 동일한 반복문 안에 있을 때만 가능합니다.SoA가 인터리브를 이기는 이유
SoA가 승리하는 이유는 다음과 같습니다:
- 속성 조회가 끌어올려짐(Hoisted) — JIT가
points.x,points.y,points.z해석을 루프 밖으로 이동시킵니다. 루프 내부에서는 인덱스 접근만 남습니다.
- 더 깔끔한 루프 본문 — 매 반복마다
i * 3곱셈 연산이 필요 없습니다.
- 현대적인 프리페처의 다중 스트림 처리 — CPU는 여러 순차적 접근 패턴을 감지하고 모두 미리 가져오는 데 능숙합니다. 세 개의 별도 배열은 문제가 되지 않습니다.
제 생각에 인터리브 패턴이 지는 이유는
i * 3 산술 오버헤드와 속성 조회를 끌어올리는 이점을 동일하게 누리지 못하기 때문입니다.최종 벤치마크: 대규모 데이터에서의 모든 패턴
function main() { const ARRAY_SIZE = 50_000_000; const aos = []; for (let i = 0; i < ARRAY_SIZE; i++) { aos.push({ x: i, y: i * 2, z: i * 3 }); } const soa = { x: new Float64Array(ARRAY_SIZE), y: new Float64Array(ARRAY_SIZE), z: new Float64Array(ARRAY_SIZE) }; for (let i = 0; i < ARRAY_SIZE; i++) { soa.x[i] = i; soa.y[i] = i * 2; soa.z[i] = i * 3; } const interleaved = new Float64Array(ARRAY_SIZE * 3); for (let i = 0; i < ARRAY_SIZE; i++) { const base = i * 3; interleaved[base] = i; interleaved[base + 1] = i * 2; interleaved[base + 2] = i * 3; } let sumAoS = 0; const startAoS = performance.now(); for (let iter = 0; iter < 10; iter++) { for (let i = 0; i < ARRAY_SIZE; i++) { sumAoS += aos[i].x + aos[i].y + aos[i].z; } } const timeAoS = performance.now() - startAoS; let sumSoA = 0; const startSoA = performance.now(); for (let iter = 0; iter < 10; iter++) { for (let i = 0; i < ARRAY_SIZE; i++) { sumSoA += soa.x[i] + soa.y[i] + soa.z[i]; } } const timeSoA = performance.now() - startSoA; let sumInterleaved = 0; const startInterleaved = performance.now(); for (let iter = 0; iter < 10; iter++) { for (let i = 0; i < ARRAY_SIZE; i++) { const base = i * 3; sumInterleaved += interleaved[base] + interleaved[base + 1] + interleaved[base + 2]; } } const timeInterleaved = performance.now() - startInterleaved; console.log(`AoS: ${timeAoS.toFixed(2)}ms`); console.log(`SoA: ${timeSoA.toFixed(2)}ms`); console.log(`Interleaved: ${timeInterleaved.toFixed(2)}ms`);}main();결과:
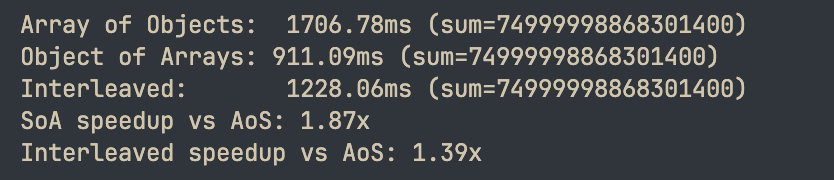
5,000만 개의 요소에서도 SoA가 여전히 가장 빠릅니다.
실제로 중요한 것들의 요약
중요하다고 생각했던 것들:
인터리브 대 SoA의 캐시 지역성(프리페처가 다중 스트림을 잘 처리함)
TypedArray가 본질적으로 일반 배열보다 빠름(V8은 숫자 배열을 동일하게 잘 최적화함)
push() 대 사전 할당(읽기 성능에는 차이가 없음)
실제로 중요한 것들:
- 요소당 객체 오버헤드 제거 — 이것이 가장 큰 승리 요인입니다 (~5-6배).
- 루프 오버헤드 — 각 반복에서 더 많은 작업을 수행하여 반복 횟수를 줄이는 것이 더 빠릅니다.
- 속성 접근 끌어올리기(Hoisting) — SoA 패턴은 JIT가 더 잘 최적화할 수 있게 해줍니다.
- TypedArray의 보장 — 순수 속도 때문이 아니라, "일관된" 성능을 위해서입니다.
맺음말
CPU는 여러 선형 메모리 스트림을 쉽게 유지할 수 있으므로, 수천만 개의 요소에서도 세 개의 배열을 건드리는 것은 문제가 되지 않는다고 생각합니다. 물론 더 테스트해 봐야겠지만요. 또한, 인터리브 레이아웃은 추가적인 인덱스 산술 연산(
i * 3)을 유발하고, SoA와 같은 수준의 끌어올리기 및 깔끔한 벡터화를 방해하여 공간 지역성이 좋음에도 불구하고 성능을 약간 떨어뜨리는 복합적인 오버헤드를 만듭니다.^ 이것은 저의 가설이며, 실제 원인을 찾고 벤치마크로 검증하기 위해 더 깊이 파고들어야 할 것입니다.
저는 여전히 이러한 것들에 대해 배우는 중이며 계속해서 발견한 내용을 포스팅할 예정입니다. 질문이나 아이디어, 요청 사항이 있다면 언제든지 연락해 주세요!
0
6
댓글
?
아직 댓글이 없습니다.
첫 번째 댓글을 작성해보세요!
Inkyu Oh님의 다른 글
더보기
번역
TypeScript 성능 문제 해결: 사례 연구
Inkyu Oh • Front-End
0
0
9
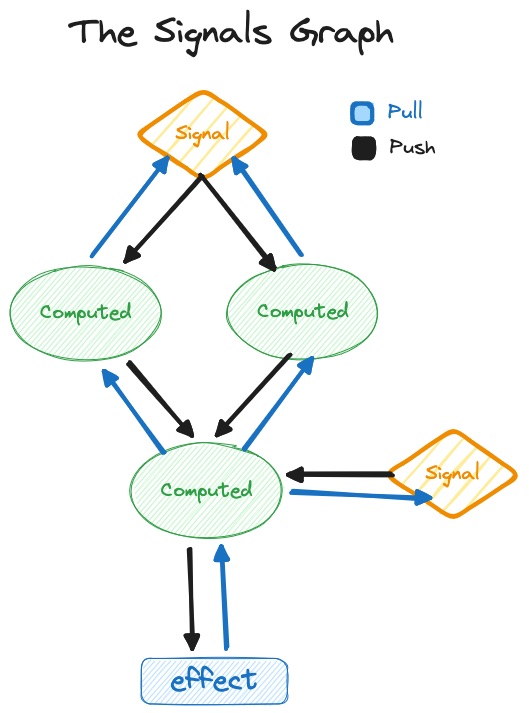
번역
시그널(Signals) vs 쿼리 기반 컴파일러(Query-Based Compilers)
Inkyu Oh • SW Engineering
0
0
10

번역
AI 에이전트를 위한 좋은 스펙 작성법
Inkyu Oh • AI & ML-ops
0
0
278

번역
GraphQL 에러 처리 가이드
Inkyu Oh • 라이브러리, 프레임워크
0
0
8